RankSobolSensitivityAlgorithm¶
- class RankSobolSensitivityAlgorithm(*args)¶
Sensitivity analysis using rank-based method.
- Parameters:
Notes
This method allows one to compute the first order Sobol’ indices given some input / output samples [gamboa2022]. It is not yet extended to higher order indices as well as total order indices.
Considering the input random vector
and let
be the output of the physical model:
In the following description Y is considered as scalar, without loss of generality.
Main assumptions:
are independent and scalar
We want to estimate the first order Sobol’ index
with respect to
for
Let’s consider a i.i.d. N-sample of the input/output pair
given by:
The pairs
are ranked (noted using lower scripts under brackets) in such a way that:
The first order Sobol’ indices estimated based on ranks are given by:
where the permutation is defined such that
.
Confidence intervals are obtained via bootstrap without replacement.
The ratio of the bootstrap’s sample size with respect to the total size of the input sample is fixed in the RankSobolSensitivityAlgorithm-DefaultBootstrapSampleRatio ResourceMap key.
Examples
>>> import openturns as ot >>> import openturns.experimental as otexp >>> from openturns.usecases import ishigami_function >>> im = ishigami_function.IshigamiModel() >>> x = im.distributionX.getSample(100) >>> y = im.model(x) >>> algo = otexp.RankSobolSensitivityAlgorithm(x, y) >>> indices = algo.getFirstOrderIndices()
Methods
DrawCorrelationCoefficients(*args)Draw the correlation coefficients.
DrawImportanceFactors(*args)Draw the importance factors.
DrawSobolIndices(*args)Draw the Sobol' indices.
draw()Draw sensitivity indices.
Get the evaluation of aggregated first order Sobol indices.
Method not yet implemented.
Get the number of bootstrap sampling size.
Accessor to the object's name.
Get the confidence interval level for confidence intervals.
getFirstOrderIndices([marginalIndex])Get first order Sobol indices.
Get the distribution of the aggregated first order Sobol indices.
Get interval for the aggregated first order Sobol indices.
getName()Accessor to the object's name.
getSecondOrderIndices([marginalIndex])Method not yet implemented.
getTotalOrderIndices([marginalIndex])Method not yet implemented.
Method not yet implemented.
Method not yet implemented.
Method not yet implemented.
hasName()Test if the object is named.
setBootstrapSize(bootstrapSize)Set the number of bootstrap sampling size.
setConfidenceLevel(confidenceLevel)Set the confidence interval level for confidence intervals.
setDesign(inputDesign, outputDesign, size)Sample accessor.
setName(name)Accessor to the object's name.
Method not yet implemented.
- __init__(*args)¶
- static DrawCorrelationCoefficients(*args)¶
- Draw the correlation coefficients.
As correlation coefficients are considered, values might be positive or negative.
- Available usages:
DrawCorrelationCoefficients(correlationCoefficients, title=’Correlation coefficients’)
DrawCorrelationCoefficients(values, names, title=’Correlation coefficients’)
- Parameters:
- correlationCoefficients
PointWithDescription Sequence containing the correlation coefficients with a description for each component. The descriptions are used to build labels for the created graph. If they are not mentioned, default labels will be used.
- valuessequence of float
Correlation coefficients.
- namessequence of str
Variables’ names used to build labels for the created the graph.
- titlestr
Title of the graph.
- correlationCoefficients
- Returns:
- static DrawImportanceFactors(*args)¶
Draw the importance factors.
- Available usages:
DrawImportanceFactors(importanceFactors, title=’Importance Factors’)
DrawImportanceFactors(values, names, title=’Importance Factors’)
- Parameters:
- importanceFactors
PointWithDescription Sequence containing the importance factors with a description for each component. The descriptions are used to build labels for the created Pie. If they are not mentioned, default labels will be used.
- valuessequence of float
Importance factors.
- namessequence of str
Variables’ names used to build labels for the created Pie.
- titlestr
Title of the graph.
- importanceFactors
- Returns:
- static DrawSobolIndices(*args)¶
Draw the Sobol’ indices.
- Parameters:
- Returns:
- graph
Graph For each variable, draws first and total indices
- graph
- draw()¶
Draw sensitivity indices.
- Usage:
draw()
Draw the aggregated first order Sobol’ indices.
- Returns:
- graph
Graph A graph containing the aggregated first and total order indices.
- graph
Notes
If number of bootstrap sampling is greater than 1, the graph includes confidence interval plots in the first usage. This is defined in the SobolIndicesAlgorithm-DefaultBootstrapSize ResourceMap key.
- getAggregatedFirstOrderIndices()¶
Get the evaluation of aggregated first order Sobol indices.
- Returns:
- indices
Point Sequence containing aggregated first order Sobol indices.
- indices
- getAggregatedTotalOrderIndices()¶
Method not yet implemented.
- getBootstrapSize()¶
Get the number of bootstrap sampling size.
- Returns:
- bootstrapSizeint
Number of bootstrap sampling
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getConfidenceLevel()¶
Get the confidence interval level for confidence intervals.
- Returns:
- confidenceLevelfloat
Confidence level for confidence intervals
- getFirstOrderIndices(marginalIndex=0)¶
Get first order Sobol indices.
- Parameters:
- marginalIndexint, optional
Index of the output marginal of the function, equal to
by default.
- Returns:
- indices
Point Sequence containing first order Sobol indices.
- indices
- getFirstOrderIndicesDistribution()¶
Get the distribution of the aggregated first order Sobol indices.
- Returns:
- distribution
Distribution Distribution for first order Sobol indices for each component.
- distribution
- getFirstOrderIndicesInterval()¶
Get interval for the aggregated first order Sobol indices.
- Returns:
- interval
Interval Interval for first order Sobol indices for each component. Computed marginal by marginal (not from the joint distribution).
- interval
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getSecondOrderIndices(marginalIndex=0)¶
Method not yet implemented.
- getTotalOrderIndices(marginalIndex=0)¶
Method not yet implemented.
- getTotalOrderIndicesDistribution()¶
Method not yet implemented.
- getTotalOrderIndicesInterval()¶
Method not yet implemented.
- getUseAsymptoticDistribution()¶
Method not yet implemented.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setBootstrapSize(bootstrapSize)¶
Set the number of bootstrap sampling size.
Default value is 0.
- Parameters:
- bootstrapSizeint
Number of bootstrap sampling
- setConfidenceLevel(confidenceLevel)¶
Set the confidence interval level for confidence intervals.
- Parameters:
- confidenceLevelfloat
Confidence level for confidence intervals
- setDesign(inputDesign, outputDesign, size)¶
Sample accessor.
Allows one to estimate indices from a predefined Sobol design.
- Parameters:
- inputDesign
Sample Design for the evaluation of sensitivity indices, obtained thanks to the SobolIndicesAlgorithmImplementation.Generate method
- outputDesign
Sample Design for the evaluation of sensitivity indices, obtained as the evaluation of a Function (model) on the previous inputDesign
- Nint
Base size of the Sobol design
- inputDesign
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setUseAsymptoticDistribution(arg2)¶
Method not yet implemented.
Examples using the class¶
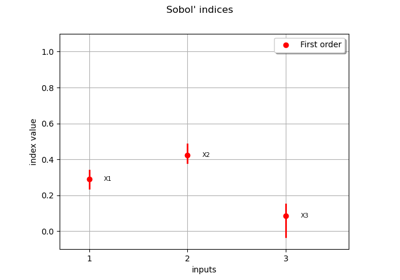
Sobol’ sensitivity indices using rank-based algorithm
Example of sensitivity analyses on the wing weight model
 OpenTURNS
OpenTURNS