SimulationAlgorithm¶
- class SimulationAlgorithm(*args)¶
Base class for simulation algorithms.
Methods
Accessor to the block size.
Accessor to the object's name.
Accessor to the convergence strategy.
Accessor to the maximum coefficient of variation.
Accessor to the maximum iterations number.
Accessor to the maximum standard deviation.
Accessor to the maximum duration.
getName()Accessor to the object's name.
hasName()Test if the object is named.
run()Launch simulation.
setBlockSize(blockSize)Accessor to the block size.
setConvergenceStrategy(convergenceStrategy)Accessor to the convergence strategy.
Accessor to the maximum coefficient of variation.
setMaximumOuterSampling(maximumOuterSampling)Accessor to the maximum iterations number.
Accessor to the maximum standard deviation.
setMaximumTimeDuration(maximumTimeDuration)Accessor to the maximum duration.
setName(name)Accessor to the object's name.
setProgressCallback(*args)Set up a progress callback.
setStopCallback(*args)Set up a stop callback.
- __init__(*args)¶
- getBlockSize()¶
Accessor to the block size.
- Returns:
- blockSizeint
Number of simultaneous evaluations of the limit-state function. It is set by default to 1.
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getConvergenceStrategy()¶
Accessor to the convergence strategy.
- Returns:
- storage_strategy
HistoryStrategy Storage strategy used to store the values of the probability estimator and its variance during the simulation algorithm.
- storage_strategy
- getMaximumCoefficientOfVariation()¶
Accessor to the maximum coefficient of variation.
- Returns:
- coefficientfloat
Maximum coefficient of variation of the simulated sample.
- getMaximumOuterSampling()¶
Accessor to the maximum iterations number.
- Returns:
- outerSamplingint
Maximum number of iterations, each iteration performing a block of evaluations.
- getMaximumStandardDeviation()¶
Accessor to the maximum standard deviation.
- Returns:
- sigmafloat,
Maximum standard deviation of the estimator.
- sigmafloat,
- getMaximumTimeDuration()¶
Accessor to the maximum duration.
- Returns:
- maximumTimeDurationfloat
Maximum optimization duration in seconds.
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- run()¶
Launch simulation.
Notes
It launches the simulation on a sample of size at most outerSampling * blockSize, this sample being built by blocks of size blockSize. It allows one to use efficiently the distribution of the computation as well as it allows one to deal with a sample size
by a combination of blockSize and outerSampling.
- setBlockSize(blockSize)¶
Accessor to the block size.
- Parameters:
- blockSizeint,
Number of simultaneous evaluations of the limit-state function. It is set by default to 1.
- blockSizeint,
Notes
If the function supports batch evaluations this parameter can be set to the number of available CPUs to benefit from parallel execution (multithreading, multiprocessing, …); except for the Directional Sampling, where we recommend to set it to 1. It also decides the frequency of the stopping criteria and progress callbacks update as they are called once the whole block of fonction evaluations is completed.
- setConvergenceStrategy(convergenceStrategy)¶
Accessor to the convergence strategy.
- Parameters:
- storage_strategy
HistoryStrategy Storage strategy used to store the values of the probability estimator and its variance during the simulation algorithm.
- storage_strategy
- setMaximumCoefficientOfVariation(maximumCoefficientOfVariation)¶
Accessor to the maximum coefficient of variation.
- Parameters:
- coefficientfloat
Maximum coefficient of variation of the simulated sample.
- setMaximumOuterSampling(maximumOuterSampling)¶
Accessor to the maximum iterations number.
- Parameters:
- outerSamplingint
Maximum number of iterations, each iteration performing a block of evaluations.
- setMaximumStandardDeviation(maximumStandardDeviation)¶
Accessor to the maximum standard deviation.
- Parameters:
- sigmafloat,
Maximum standard deviation of the estimator.
- sigmafloat,
- setMaximumTimeDuration(maximumTimeDuration)¶
Accessor to the maximum duration.
- Parameters:
- maximumTimeDurationfloat
Maximum optimization duration in seconds.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setProgressCallback(*args)¶
Set up a progress callback.
Can be used to programmatically report the progress of a simulation.
- Parameters:
- callbackcallable
Takes a float as argument as percentage of progress.
Examples
>>> import sys >>> import openturns as ot >>> experiment = ot.MonteCarloExperiment() >>> X = ot.RandomVector(ot.Normal()) >>> Y = ot.CompositeRandomVector(ot.SymbolicFunction(['X'], ['1.1*X']), X) >>> event = ot.ThresholdEvent(Y, ot.Less(), -2.0) >>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment) >>> algo.setMaximumOuterSampling(100) >>> algo.setMaximumCoefficientOfVariation(-1.0) >>> def report_progress(progress): ... sys.stderr.write('-- progress=' + str(progress) + '%\n') >>> algo.setProgressCallback(report_progress) >>> algo.run()
- setStopCallback(*args)¶
Set up a stop callback.
Can be used to programmatically stop a simulation.
- Parameters:
- callbackcallable
Returns an int deciding whether to stop or continue.
Examples
Stop a Monte Carlo simulation algorithm using a time limit
>>> import openturns as ot >>> experiment = ot.MonteCarloExperiment() >>> X = ot.RandomVector(ot.Normal()) >>> Y = ot.CompositeRandomVector(ot.SymbolicFunction(['X'], ['1.1*X']), X) >>> event = ot.ThresholdEvent(Y, ot.Less(), -2.0) >>> algo = ot.ProbabilitySimulationAlgorithm(event, experiment) >>> algo.setMaximumOuterSampling(10000000) >>> algo.setMaximumCoefficientOfVariation(-1.0) >>> algo.setMaximumTimeDuration(0.1) >>> algo.run()
Examples using the class¶
Create a process from random vectors and processes
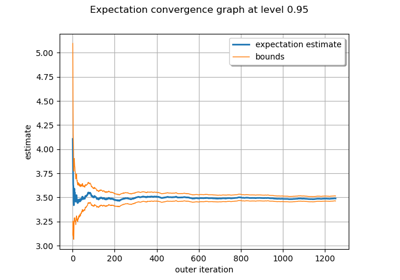
Evaluate the mean of a random vector by simulations

Use the Adaptive Directional Stratification Algorithm

Use the post-analytical importance sampling algorithm
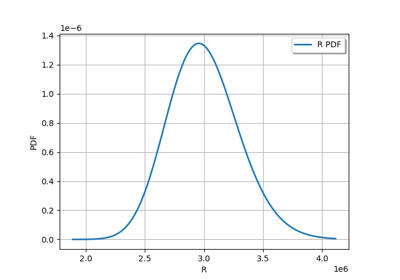
Estimate a probability with Monte-Carlo on axial stressed beam: a quick start guide to reliability
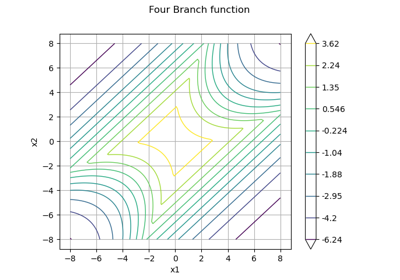
Non parametric Adaptive Importance Sampling (NAIS)
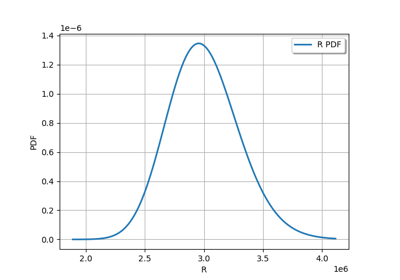
Axial stressed beam : comparing different methods to estimate a probability
Using the FORM - SORM algorithms on a nonlinear function
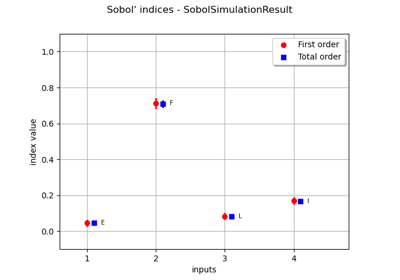
Estimate Sobol’ indices for the beam by simulation algorithm
 OpenTURNS
OpenTURNS