FunctionalChaosValidation¶

(Source code, png)

class FunctionalChaosValidation(*args)¶

Validate a functional chaos metamodel.

Warning

This class is experimental and likely to be modified in future releases. To use it, import the openturns.experimental submodule.

Parameters:

resultFunctionalChaosResult: A functional chaos result obtained from a polynomial chaos expansion.
splitterSplitterImplementation, optional: The cross-validation method. The default is LeaveOneOutSplitter.

Methods

`computeMeanSquaredError`()	Accessor to the mean squared error.
`computeR2Score`()	Compute the R2 score.
`drawValidation`()	Plot a model vs metamodel graph for visual validation.
`getClassName`()	Accessor to the object's name.
`getFunctionalChaosResult`()	Result accessor.
`getMetamodelPredictions`()	Accessor to the output predictions from the metamodel.
`getName`()	Accessor to the object's name.
`getOutputSample`()	Accessor to the output sample.
`getResidualDistribution`([smooth])	Compute the non parametric distribution of the residual sample.
`getResidualSample`()	Compute the residual sample.
`getSplitter`()	Get the cross-validation method.
`hasName`()	Test if the object is named.
`setName`(name)	Accessor to the object's name.

See also

openturns.FunctionalChaosAlgorithm, openturns.FunctionalChaosResult

Notes

A FunctionalChaosValidation object is used for the validation of a functional chaos expansion. It is based on the fast (analytical) leave-one-out and fast K-Fold cross-validation methods presented in Cross validation of PCE models.

Analytical cross-validation can only be performed accurately if some conditions are met.

This can only be done if the coefficients of the expansion are estimated using least squares regression: if the expansion is computed from integration, then an exception is produced.
This can only be done if the coefficients of the expansion are estimated using full expansion, without model selection: if the expansion is computed with model selection, then an exception is produced by default. This is because model selection leads to supposedly improved coefficients, so that the hypotheses required to estimate the mean squared error using the cross-validation method are not satisfied anymore. As a consequence, using the analytical formula without taking model selection into account leads to a biased, overly optimistic, mean squared error. More precisely, the analytical formula produces a MSE which is lower than the true one on average. Model selection is involved in the expansion if the LeastSquaresMetaModelSelectionFactory or CleaningStrategy classes are involved. If the PenalizedLeastSquaresAlgorithmFactory class is used, then no model selection is involved and the analytical cross-validation methods can be used. If model selection is involved, the naive methods based on the LeaveOneOutSplitter and KFoldSplitter classes can be used, but this can be much slower than the analytical methods implemented in the FunctionalChaosValidation class. In many cases, however, the order of magnitude of the estimate from the analytical formula applied to a sparse model is correct: the estimate of the MSE is only slightly lower than the true value. In order to enable the calculation of the analytical MSE estimator on a sparse model, please set the FunctionalChaosValidation-ModelSelection key of the ResourceMap to True: use this option at your own risks.

We suggest to use leave-one-out (LOO) cross validation when possible, because it produces a more accurate estimate of the error than K-Fold does. If K-Fold is required, we suggest to use the largest possible value of $k$ .

The predictions of the leave-one-one or K-Fold surrogate models are based on the hold-out method. For example, if we use the leave-one-out cross-validation method, the $i$ -th prediction is the prediction of the linear model trained using the hold-out sample where the $i$ -th observation was removed. This produces a sample of residuals which can be retrieved using the getResidualSample() method. The drawValidation() method performs similarly.

If the weights of the observations are not equal, the analytical method may not necessarily provide an accurate estimator of the mean squared error (MSE). This is because LOO and K-Fold cross-validation do not take the weights into account. Since the FunctionalChaosResult object does not know if the weights are equal, no exception can be generated.

If the sample was not produced from Monte Carlo, then the leave-one-out cross-validation method may not necessarily provide an accurate estimator of the MSE. Indeed, one assumption for cross validation using LOO or K-Fold is to have independent observations, which is required to state that the LOO sample MSE is an estimator of the true MSE. For example, using cross-validation on a quasi-Monte Carlo (QMC) experiment may not necessarily provide an accurate estimate of the MSE, because the internal structure of the QMC is broken by the different splits: the elementary volumes are not filled as expected anymore and the space-filling properties of the sequence are lost.

Examples

Create a polynomial chaos for the Ishigami function. We use the PenalizedLeastSquaresAlgorithmFactory class to specify the method to compute the coefficients. We may use the LeastSquaresMetaModelSelectionFactory class in order to create a sparse polynomial chaos expansion, but this prevents us from using the fast analytical formulas and get an accurate estimator of the MSE.

>>> import openturns as ot
>>> import openturns.experimental as otexp
>>> from math import pi
>>> from openturns.usecases import ishigami_function
>>> im = ishigami_function.IshigamiModel()
>>> sampleSize = 500 
>>> inputTrain = im.inputDistribution.getSample(sampleSize)
>>> outputTrain = im.model(inputTrain)
>>> multivariateBasis = ot.OrthogonalProductPolynomialFactory([im.X1, im.X2, im.X3])
>>> selectionAlgorithm = ot.PenalizedLeastSquaresAlgorithmFactory()
>>> projectionStrategy = ot.LeastSquaresStrategy(inputTrain, outputTrain, selectionAlgorithm)
>>> totalDegree = 8
>>> enumerateFunction = multivariateBasis.getEnumerateFunction()
>>> basisSize = enumerateFunction.getStrataCumulatedCardinal(totalDegree)
>>> adaptiveStrategy = ot.FixedStrategy(multivariateBasis, basisSize)
>>> chaosalgo = ot.FunctionalChaosAlgorithm(
...     inputTrain, outputTrain, im.inputDistribution, adaptiveStrategy, projectionStrategy
... )
>>> chaosalgo.run()
>>> result = chaosalgo.getResult()

Validate the polynomial chaos expansion using leave-one-out cross-validation.

>>> splitterLOO = ot.LeaveOneOutSplitter(sampleSize)
>>> validation = otexp.FunctionalChaosValidation(result, splitterLOO)
>>> r2Score = validation.computeR2Score()
>>> print('R2 = ', r2Score[0])
R2 =  0.99...

Validate the polynomial chaos expansion using K-Fold cross-validation and set the $k$ parameter.

>>> kParameter = 10
>>> splitterKF = ot.KFoldSplitter(sampleSize, kParameter)
>>> validation = otexp.FunctionalChaosValidation(
...     result, splitterKF
... )

Draw the validation graph.

>>> graph = validation.drawValidation()

__init__(*args)¶

computeMeanSquaredError()¶

Accessor to the mean squared error.

Returns:

meanSquaredErrorPoint: The mean squared error of each marginal output dimension.

Notes

The sample mean squared error is:

$\widehat{\operatorname{MSE}} = \frac{1}{n} \sum_{j=1}^{n} \left(y^{(j)} - \tilde{g}\left(\bdx^{(j)}\right)\right)^2$

where $n \in \Nset$ is the sample size, $\tilde{g}$ is the metamodel, $\{\bdx^{(j)} \in \Rset^{n_X}\}_{j = 1, ..., n}$ is the input experimental design and $\{y^{(j)} \in \Rset\}_{j = 1, ..., n}$ is the output of the model.

If the output is multi-dimensional, the same calculations are repeated separately for each output marginal $k$ for $k = 1, ..., n_y$ where $n_y \in \Nset$ is the output dimension.

computeR2Score()¶

Compute the R2 score.

Returns:

r2ScorePoint: The coefficient of determination R2

Notes

The coefficient of determination $R^2$ is the fraction of the variance of the output explained by the metamodel. It is defined as:

$R^2 = 1 - \operatorname{FVU}$

where $\operatorname{FVU}$ is the fraction of unexplained variance:

$\operatorname{FVU} = \frac{\operatorname{MSE}(\tilde{g}) }{\Var{Y}}$

where $Y = g(\bdX)$ is the output of the physical model $g$ , $\Var{Y}$ is the variance of the output and $\operatorname{MSE}$ is the mean squared error of the metamodel:

$\operatorname{MSE}(\tilde{g}) = \Expect{\left(g(\bdX) - \tilde{g}(\bdX) \right)^2}.$

The sample $R^2$ is:

$\hat{R}^2 = 1 - \frac{\frac{1}{n} \sum_{j=1}^{n} \left(y^{(j)} - \tilde{g}\left(\bdx^{(j)}\right)\right)^2}{\hat{\sigma}^2_Y}$

where $n \in \Nset$ is the sample size, $\tilde{g}$ is the metamodel, $\left\{\bdx^{(j)} \in \Rset^{n_X}\right\}_{j = 1, ..., n}$ is the input experimental design, $\left\{y^{(j)} \in \Rset\right\}_{j = 1, ..., n}$ is the output of the model and $\hat{\sigma}^2_Y$ is the sample variance of the output:

$\hat{\sigma}^2_Y = \frac{1}{n - 1} \sum_{j=1}^{n} \left(y^{(j)} - \overline{y}\right)^2$

where $\overline{y}$ is the output sample mean:

$\overline{y} = \frac{1}{n} \sum_{j=1}^{n} y^{(j)}.$

drawValidation()¶

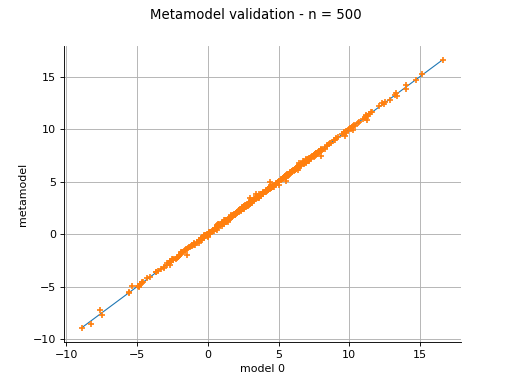
Plot a model vs metamodel graph for visual validation.

Returns:

graphGridLayout: The visual validation graph.

Notes

The plot presents the metamodel predictions depending on the model observations. If the points are close to the diagonal line of the plot, then the metamodel validation is satisfactory. Points which are far away from the diagonal represent outputs for which the metamodel is not accurate.

If the output is multi-dimensional, the graph has 1 row and $n_y \in \Nset$ columns, where $n_y$ is the output dimension.

getClassName()¶

Accessor to the object’s name.

Returns:

class_namestr: The object class name (object.__class__.__name__).

getFunctionalChaosResult()¶

Result accessor.

Returns:

resultFunctionalChaosResult: The result provided.

getMetamodelPredictions()¶

Accessor to the output predictions from the metamodel.

Returns:

outputMetamodelSampleSample: Output sample of the metamodel.

getName()¶

Accessor to the object’s name.

Returns:

namestr: The name of the object.

getOutputSample()¶

Accessor to the output sample.

Returns:

outputSampleSample: Output sample of a model evaluated apart.

getResidualDistribution(smooth=True)¶

Compute the non parametric distribution of the residual sample.

Parameters:

smoothbool: Tells if distribution is smooth (true) or not. Default argument is true.

Returns:

residualDistributionDistribution: The residual distribution.

Notes

The residual distribution is built thanks to KernelSmoothing if smooth argument is true. Otherwise, an histogram distribution is returned, thanks to HistogramFactory.

getResidualSample()¶

Compute the residual sample.

Returns:

residualSample: The residual sample.

Notes

The residual sample is given by :

$r^{(j)} = y^{(j)} - \tilde{g}\left(\vect{x}^{(j)}\right)$

for $j = 1, ..., n$ where $n \in \Nset$ is the sample size, $y^{(j)}$ is the model observation, $\tilde{g}$ is the metamodel and $\vect{x}^{(j)}$ is the $j$ -th input observation.

If the output is multi-dimensional, the residual sample has dimension $n_y \in \Nset$ , where $n_y$ is the output dimension.

getSplitter()¶

Get the cross-validation method.

Returns:

splitterSplitterImplementation: The cross-validation method.

hasName()¶

Test if the object is named.

Returns:

hasNamebool: True if the name is not empty.

setName(name)¶

Accessor to the object’s name.

Parameters:

namestr: The name of the object.

OpenTURNS

An Open source initiative for the Treatment of Uncertainties, Risks'N Statistics

Previous topic

Next topic

This Page

FunctionalChaosValidation¶