BasisFactory¶
- class BasisFactory(*args)¶
Basis factory base class.
- Parameters:
- orthogUniVarPolFactory
OrthogonalUniVariatePolynomialFactory Factory that builds particular univariate polynomial (e.g. Hermite, Legendre, Laguerre, …).
- orthogUniVarPolFactory
Methods
build()Build the basis.
Accessor to the object's name.
getName()Accessor to the object's name.
hasName()Test if the object is named.
setName(name)Accessor to the object's name.
Notes
BasisFactory is the interface of the OrthogonalUniVariatePolynomialFactory implementation. It represents the factory that allows the construction of any univariate orthonormal polynomial with any degree.
- __init__(*args)¶
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
Examples using the class¶
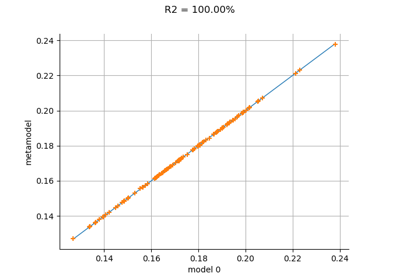
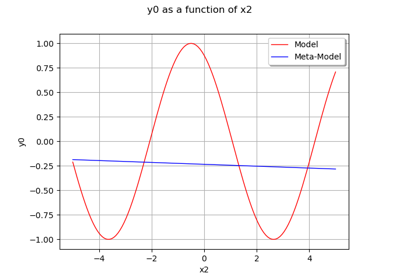
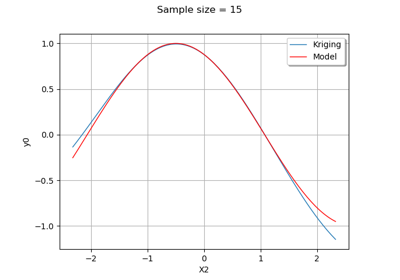
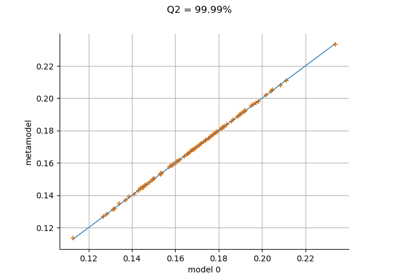
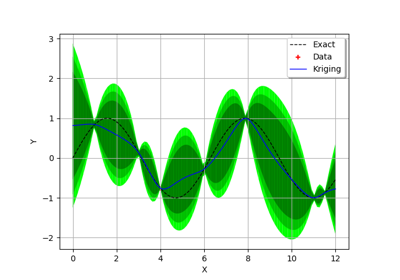
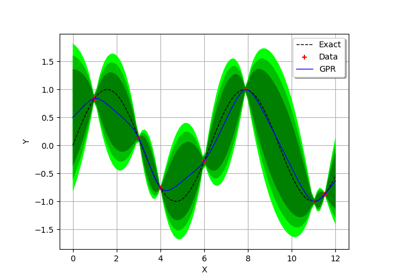
Gaussian Process Regression : cantilever beam model
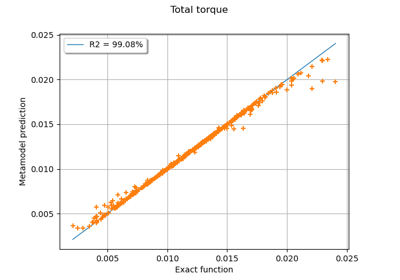
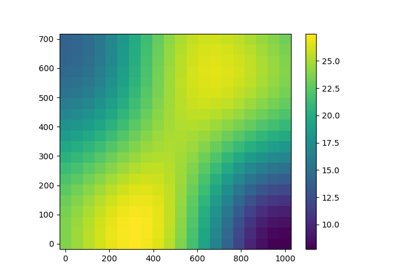
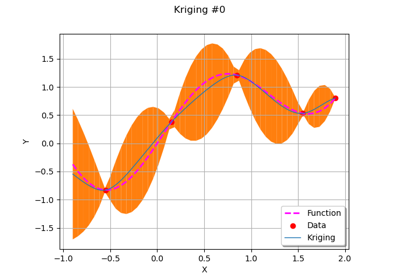
Example of multi output Kriging on the fire satellite model
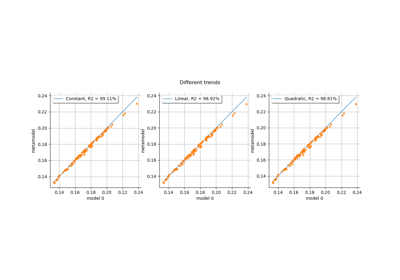
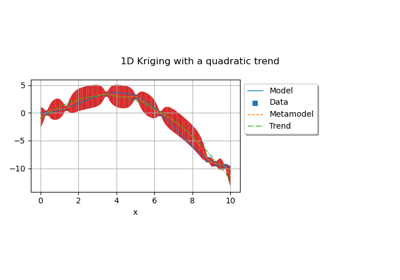
Kriging: choose a polynomial trend on the beam model
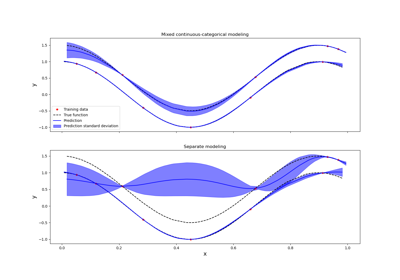
Kriging: metamodel with continuous and categorical variables
 OpenTURNS
OpenTURNS