Analytical¶
- class Analytical(*args)¶
Base class to evaluate the probability of failure of a system.
- Parameters:
- nearestPointAlgorithm
OptimizationAlgorithm Optimization algorithm used to search the design point.
- event
RandomVector Failure event.
- physicalStartingPointsequence of float
Starting point of the optimization algorithm, declared in the physical space.
- nearestPointAlgorithm
Methods
Accessor to the result.
Accessor to the object's name.
getEvent()Accessor to the event of which the probability is calculated.
getName()Accessor to the object's name.
Accessor to the optimization algorithm used to find the design point.
Accessor to the starting point of the optimization algorithm.
hasName()Test if the object is named.
run()Perform the research of the design point.
setEvent(event)Accessor to the event of which the probability is calculated.
setName(name)Accessor to the object's name.
setNearestPointAlgorithm(solver)Accessor to the optimization algorithm used to find the design point.
setPhysicalStartingPoint(physicalStartingPoint)Accessor to the starting point of the optimization algorithm.
See also
Notes
Used in reliability analysis, Analytical is a base class for the approximation methods
FORMandSORMenabling to evaluate the failure probability of a system. A failure event is defined as follows :where
denotes a random input vector representing the sources of uncertainties,
is a determinist vector representing the fixed variables.
is the limit state function of the model separating the failure domain from the safe domain. Considering
the joint probability density function of the random variables
, the probability of failure of the event
is :
The analytical methods use an isoprobabilistic transformation to move from the physical space to the standard normal space (U-space) where distributions are spherical (invariant by rotation by definition), with zero mean, unit variance and unit correlation matrix. The usual isoprobabilistic transformations are the Generalized Nataf transformation and the Rosenblatt one.
In that new U-space, the event has the new expression defined from the transformed limit state function of the model
and its boundary :
. Then, the event probability
rewrites :
where
is the density function of the distribution in the standard space.
The analytical methods rely on the assumption that most of the contribution to
comes from points located in the vicinity of a particular point
, the design point, defined in the U-space as the point located on the limit state surface verifying the event of maximum likelihood. Given the probabilistic characteristics of the U-space,
has a geometrical interpretation: it is the point located on the event boundary and at minimal distance from the origin of the U-space. Thus, considering
its coordinates in the U-space, the design point is the result of the constrained optimization problem :
Then the limit state surface is approximated in the standard space by a linear surface (
FORM) or by a quadratic surface (SORM) at the design point in order to evaluate the failure probability. For more information on this evaluation, see the documentation associated with these two methods.The result of the optimization problem is recoverable thanks to the method
getAnalyticalResult().The unicity and the strongness of the design point can be checked thanks to the
Strong Maximum Test.An absolute tolerance on the limit state (in the physical space) is implemented to check if the design point found by the algorithm can be used to accurately estimate the failure probability, that is if:
where
is the design point,
is the threshold and
is the absolute tolerance. Default value is specified in the nearestPointAlgorithm attribute.
Examples
>>> import openturns as ot >>> myFunction = ot.SymbolicFunction(['E', 'F', 'L', 'I'], ['-F*L^3/(3*E*I)']) >>> myDistribution = ot.Normal([50.0, 1.0, 10.0, 5.0], [1.0]*4, ot.IdentityMatrix(4)) >>> vect = ot.RandomVector(myDistribution) >>> output = ot.CompositeRandomVector(myFunction, vect) >>> myEvent = ot.ThresholdEvent(output, ot.Less(), -3.0) >>> # We create an OptimizationAlgorithm algorithm >>> myOptim = ot.AbdoRackwitz() >>> myAlgo = ot.Analytical(myOptim, myEvent, [50.0, 1.0, 10.0, 5.0])
- __init__(*args)¶
- getAnalyticalResult()¶
Accessor to the result.
- Returns:
- result
AnalyticalResult Result structure which contains the results of the optimisation problem.
- result
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getEvent()¶
Accessor to the event of which the probability is calculated.
- Returns:
- event
RandomVector Event of which the probability is calculated.
- event
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getNearestPointAlgorithm()¶
Accessor to the optimization algorithm used to find the design point.
- Returns:
- algorithm
OptimizationAlgorithm Optimization algorithm used to research the design point.
- algorithm
- getPhysicalStartingPoint()¶
Accessor to the starting point of the optimization algorithm.
- Returns:
- point
Point Starting point of the optimization algorithm, declared in the physical space.
- point
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- run()¶
Perform the research of the design point.
Notes
Performs the research of the design point and creates a
AnalyticalResult, the structure result which is accessible with the methodgetAnalyticalResult().
- setEvent(event)¶
Accessor to the event of which the probability is calculated.
- Parameters:
- event
RandomVector Event of which the probability is calculated.
- event
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setNearestPointAlgorithm(solver)¶
Accessor to the optimization algorithm used to find the design point.
- Parameters:
- algorithm
OptimizationAlgorithm Optimization algorithm used to research the design point.
- algorithm
- setPhysicalStartingPoint(physicalStartingPoint)¶
Accessor to the starting point of the optimization algorithm.
- Parameters:
- pointsequence of float
Starting point of the optimization algorithm, declared in the physical space.
Examples using the class¶

Use the post-analytical importance sampling algorithm
Use the FORM algorithm in case of several design points

Test the design point with the Strong Maximum Test
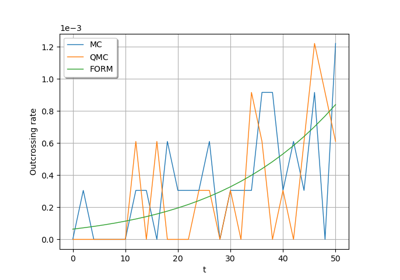
Axial stressed beam : comparing different methods to estimate a probability
An illustrated example of a FORM probability estimate
Using the FORM - SORM algorithms on a nonlinear function
 OpenTURNS
OpenTURNS