Estimate the probability of a threshold excedance

A load is applied to a cantilever beam. For construction reasons, the beam must not exceed a bending of 30 cm. The load (F), beam Young’s modulus (E), length (L) and section modulus (I) are uncertain.

---

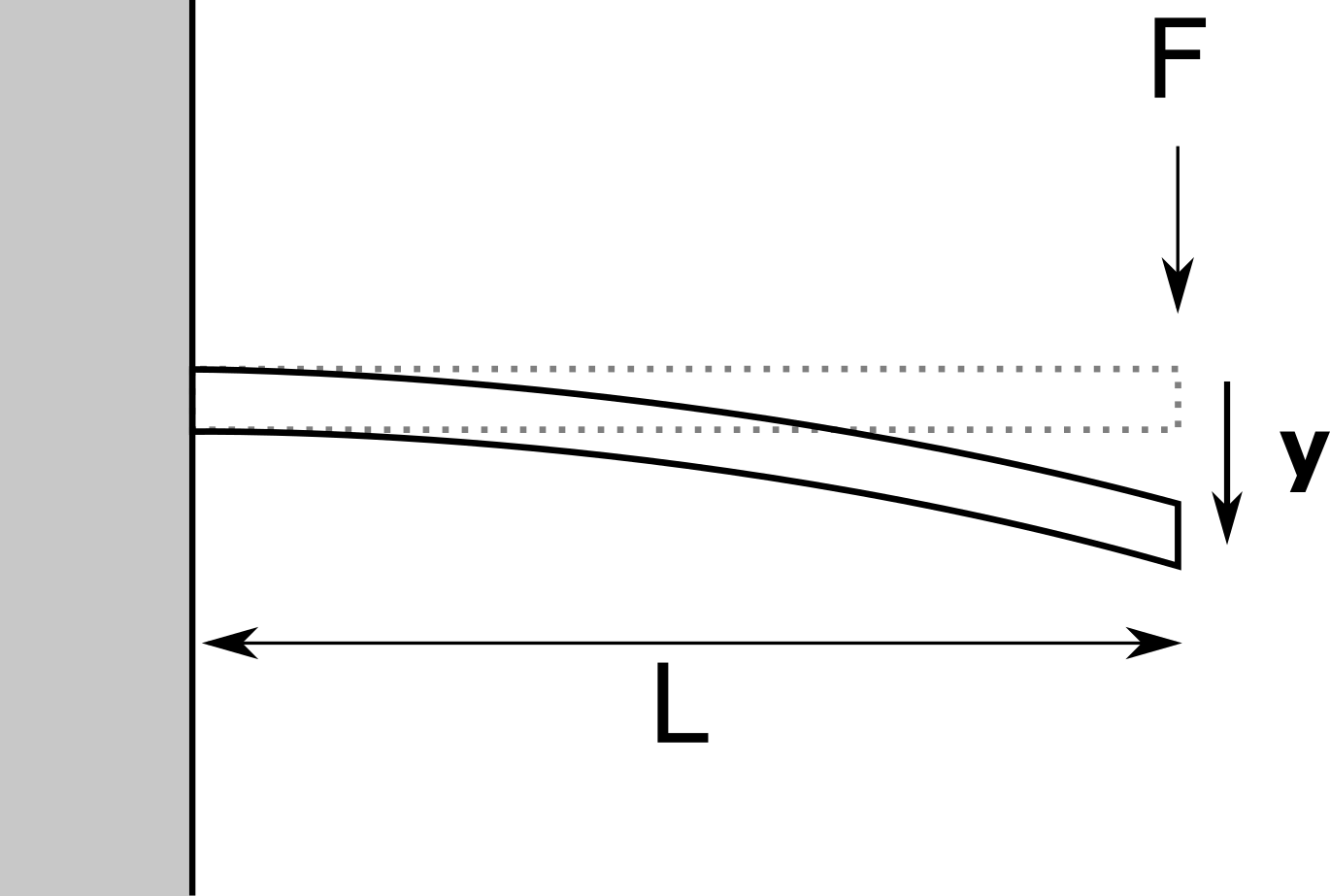
See the cantilever beam model here.

---

What is the probability that the deviation exceeds the threshold ?

We load the FMU as a FMUFunction (see the tutorial):

import openturns as ot
import otfmi
import otfmi.example.utility
import openturns.viewer as otv

path_fmu = otfmi.example.utility.get_path_fmu("deviation")

model_fmu = otfmi.FMUFunction(
    path_fmu, inputs_fmu=["E", "F", "L", "I"], outputs_fmu="y"
)

We test the function wrapping the deviation model on a point:

point = ot.Point([3e7, 2e4, 255, 350])
model_evaluation = model_fmu(point)
print(f"Running the FMU: deviation = {model_evaluation}")

Running the FMU: deviation = [10.5279]

We define probability laws on the 4 uncertain inputs:

E = ot.Beta(0.93, 3.2, 2.8e7, 4.8e7)
F = ot.LogNormal()
F.setParameter(ot.LogNormalMuSigma()([30.0e3, 9e3, 15.0e3]))
L = ot.Uniform(250.0, 260.0)
II = ot.Beta(2.5, 4.0, 310.0, 450.0)

According to the laws of mechanics, when the length L increases, the moment of inertia I decreases. The variables L and I are thus negatively correlated.

We assume that the random variables E, F, L and I are dependent and associated with a gaussian copula which correlation matrix:

We implement this correlation:

# Create the Spearman correlation matrix of the input random vector
RS = ot.CorrelationMatrix(4)
RS[2, 3] = -0.2

# Evaluate the correlation matrix of the Normal copula from RS
R = ot.NormalCopula.GetCorrelationFromSpearmanCorrelation(RS)

# Create the Normal copula parametrized by R
mycopula = ot.NormalCopula(R)

And we endly create the composed input probability distribution.

inputDistribution = ot.ComposedDistribution([E, F, L, II], mycopula)
inputDistribution.setDescription(model_fmu.getInputDescription())

Create the event whose probability we want to estimate:

inputRandomVector = ot.RandomVector(inputDistribution)
outputVariableOfInterest = ot.CompositeRandomVector(model_fmu, inputRandomVector)

threshold = 30
event = ot.ThresholdEvent(outputVariableOfInterest, ot.Greater(), threshold)
event.setName("Deviation > %g cm" % threshold)

Parameterize and run the Monte Carlo algorithm:

ot.RandomGenerator.SetSeed(23091926)  # set seed for reproducibility

experiment = ot.MonteCarloExperiment()
algo = ot.ProbabilitySimulationAlgorithm(event, experiment)
algo.setMaximumOuterSampling(200)
algo.setMaximumCoefficientOfVariation(0.2)
algo.run()

Draw the distribution of threshold excedance probability:

monte_carlo_result = algo.getResult()
probabilityDistribution = monte_carlo_result.getProbabilityDistribution()
graph = otv.View(probabilityDistribution.drawPDF())

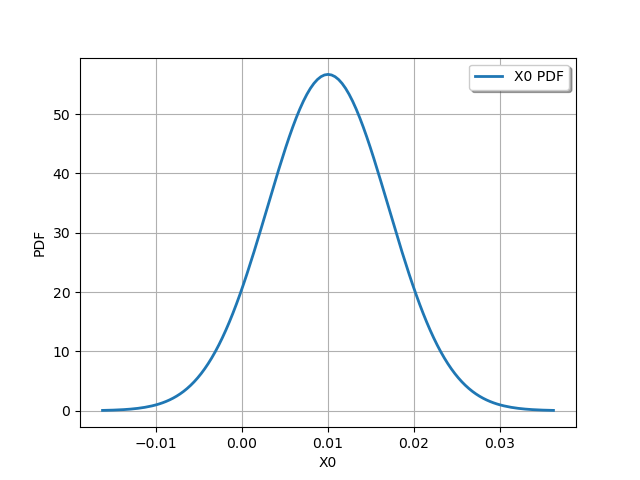
Get the probability with which the beam deviation exceeds 30 cm:

probability = monte_carlo_result.getProbabilityEstimate()
print(f"Threshold excedance probability: {probability}")

Threshold excedance probability: 0.009999999999999998

Given the uncertainties on the load applied and the beam mechanical parameters, the beam bending has a probability of 0.01 to exceed 30 cm. Is this probability low or not ? It depends on your context 🙂

otv.View.ShowAll()