MetaModelAlgorithm

class MetaModelAlgorithm(*args)

Base class for metamodel algorithms.

Parameters:

sampleX, sampleY2-d sequence of float

Input/output samples

distributionDistribution, optional

Joint probability density function of the physical input vector.

See also

LinearModelAlgorithm, KrigingAlgorithm, GeneralLinearModelAlgorithm, FunctionalChaosAlgorithm

Methods

BuildDistribution(inputSample)	Recover the distribution, with metamodel performance in mind.
getClassName()	Accessor to the object's name.
getDistribution()	Accessor to the joint probability density function of the physical input vector.
getId()	Accessor to the object's id.
getInputSample()	Accessor to the input sample.
getName()	Accessor to the object's name.
getOutputSample()	Accessor to the output sample.
getShadowedId()	Accessor to the object's shadowed id.
getVisibility()	Accessor to the object's visibility state.
hasName()	Test if the object is named.
hasVisibleName()	Test if the object has a distinguishable name.
run()	Compute the response surfaces.
setDistribution(distribution)	Accessor to the joint probability density function of the physical input vector.
setName(name)	Accessor to the object's name.
setShadowedId(id)	Accessor to the object's shadowed id.
setVisibility(visible)	Accessor to the object's visibility state.

__init__(*args)

static BuildDistribution(inputSample)

Recover the distribution, with metamodel performance in mind.

For each marginal, find the best 1-d continuous parametric model else fallback to the use of a nonparametric one.

The selection is done as follow:

• We start with a list of all parametric models (all factories)

• For each model, we estimate its parameters if feasible.

• We check then if model is valid, ie if its Kolmogorov score exceeds a threshold fixed in the MetaModelAlgorithm-PValueThreshold ResourceMap key. Default value is 5%

• We sort all valid models and return the one with the optimal criterion.

For the last step, the criterion might be BIC, AIC or AICC. The specification of the criterion is done through the MetaModelAlgorithm-ModelSelectionCriterion ResourceMap key. Default value is fixed to BIC. Note that if there is no valid candidate, we estimate a non-parametric model (KernelSmoothing or Histogram). The MetaModelAlgorithm-NonParametricModel ResourceMap key allows selecting the preferred one. Default value is Histogram

One each marginal is estimated, we use the Spearman independence test on each component pair to decide whether an independent copula. In case of non independence, we rely on a NormalCopula.

Parameters:

sampleSample

Input sample.

Returns:

distributionDistribution

Input distribution.

getClassName()

Accessor to the object’s name.

Returns:

class_namestr

The object class name (object.__class__.__name__).

getDistribution()

Accessor to the joint probability density function of the physical input vector.

Returns:

distributionDistribution

Joint probability density function of the physical input vector.

getId()

Accessor to the object’s id.

Returns:

idint

Internal unique identifier.

getInputSample()

Accessor to the input sample.

Returns:

inputSampleSample

Input sample of a model evaluated apart.

getName()

Accessor to the object’s name.

Returns:

namestr

The name of the object.

getOutputSample()

Accessor to the output sample.

Returns:

outputSampleSample

Output sample of a model evaluated apart.

getShadowedId()

Accessor to the object’s shadowed id.

Returns:

idint

Internal unique identifier.

getVisibility()

Accessor to the object’s visibility state.

Returns:

visiblebool

Visibility flag.

hasName()

Test if the object is named.

Returns:

hasNamebool

True if the name is not empty.

hasVisibleName()

Test if the object has a distinguishable name.

Returns:

hasVisibleNamebool

True if the name is not empty and not the default one.

run()

Compute the response surfaces.

Notes

It computes the response surfaces and creates a MetaModelResult structure containing all the results.

setDistribution(distribution)

Accessor to the joint probability density function of the physical input vector.

Parameters:

distributionDistribution

Joint probability density function of the physical input vector.

setName(name)

Accessor to the object’s name.

Parameters:

namestr

The name of the object.

setShadowedId(id)

Accessor to the object’s shadowed id.

Parameters:

idint

Internal unique identifier.

setVisibility(visible)

Accessor to the object’s visibility state.

Parameters:

visiblebool

Visibility flag.

Examples using the class

Build and validate a linear model

Build and validate a linear model

Create a general linear model metamodel

Create a general linear model metamodel

Create a linear model

Create a linear model

Mixture of experts

Mixture of experts

Perfom stepwise regression

Perfom stepwise regression

Fit a distribution from an input sample

Fit a distribution from an input sample

Polynomial chaos exploitation

Polynomial chaos exploitation

Polynomial chaos over database

Polynomial chaos over database

Compute grouped indices for the Ishigami function

Compute grouped indices for the Ishigami function

Validate a polynomial chaos

Validate a polynomial chaos

Create a polynomial chaos metamodel by integration on the cantilever beam

Create a polynomial chaos metamodel by integration on the cantilever beam

Advanced polynomial chaos construction

Advanced polynomial chaos construction

Create a polynomial chaos metamodel

Create a polynomial chaos metamodel

Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos

Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos

Chaos cross-validation

Chaos cross-validation

Polynomial chaos is sensitive to the degree

Polynomial chaos is sensitive to the degree

Create a sparse chaos by integration

Create a sparse chaos by integration

Compute Sobol’ indices confidence intervals

Compute Sobol' indices confidence intervals

Kriging : propagate uncertainties

Kriging : propagate uncertainties

Kriging : multiple input dimensions

Kriging : multiple input dimensions

Kriging : draw the likelihood

Kriging : draw the likelihood

Kriging : cantilever beam model

Kriging : cantilever beam model

Configuring an arbitrary trend in Kriging

Configuring an arbitrary trend in Kriging

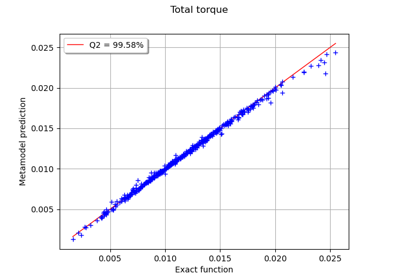
Example of multi output Kriging on the fire satellite model

Example of multi output Kriging on the fire satellite model

Kriging the cantilever beam model using HMAT

Kriging the cantilever beam model using HMAT

Kriging : generate trajectories from a metamodel

Kriging : generate trajectories from a metamodel

Choose the trend basis of a kriging metamodel

Choose the trend basis of a kriging metamodel

Kriging with an isotropic covariance function

Kriging with an isotropic covariance function

Kriging: metamodel of the Branin-Hoo function

Kriging: metamodel of the Branin-Hoo function

Kriging : quick-start

Kriging : quick-start

Sequentially adding new points to a kriging

Sequentially adding new points to a kriging

Advanced kriging

Advanced kriging

Kriging :configure the optimization solver

Kriging :configure the optimization solver

Kriging : choose a trend vector space

Kriging : choose a trend vector space

Viscous free fall: metamodel of a field function

Viscous free fall: metamodel of a field function

Metamodel of a field function

Metamodel of a field function

Sobol’ sensitivity indices from chaos

Sobol' sensitivity indices from chaos

Use the ANCOVA indices

Use the ANCOVA indices

Example of sensitivity analyses on the wing weight model

Example of sensitivity analyses on the wing weight model

EfficientGlobalOptimization examples

EfficientGlobalOptimization examples