Graph¶
- class Graph(*args)¶
Class Graph containing drawable elements and a graphical context.
- Available constructors:
Graph(title=’’)
Graph(title, xTitle, yTitle, showAxes, legendPosition=’’, legendFontSize=1.0, logScale=ot.GraphImplementation.NONE)
- Parameters:
- titlestr
Title of the graph.
- xTitlestr
Legend of the X axe.
- yTitlestr
Legend of the Y axe.
- showAxesbool
True to draw the axes. False to hide them.
- legendPositionstr
Indication of the legend’s position. If legendPosition is not specified, the Graph has no legend. The valid strings are given by the
GetValidLegendPositions()method.- legendFontSizefloat
Font size of the legend.
- logScaleint
logScale indicates whether the logarithmic scale is used either for one or both axes:
ot.GraphImplementation.NONE or 0: no log scale is used,
ot.GraphImplementation.LOGX or 1: log scale is used only for horizontal data,
ot.GraphImplementation.LOGY or 2: log scale is used only for vertical data,
ot.GraphImplementation.LOGXY or 3: log scale is used for both data.
Methods
Accessor to the list of valid legend positions.
IsValidLegendPosition(position)Test if the proposed legend position is valid or not.
add(*args)Add drawable instances to the collection of drawables contained in Graph.
erase(i)Erase a drawable instance from the collection of drawables contained in Graph.
Accessor to the indication of automatic bounding box.
getAxes()Accessor to the indication of axes' presence on the Graph.
Accessor to the bounding box of the whole plot.
Accessor to the object's name.
Accessor to the colors of the Drawables included in the Graph.
getDrawable(index)Accessor to a Drawable included in the Graph.
Accessor to the Drawables included in the Graph.
getGrid()Accessor to the indication of grid's presence on the Graph.
Accessor to the indication of grid's color on the Graph.
getId()Accessor to the object's id.
Accessor to the underlying implementation.
Accessor to the integer x-axis ticks flag.
Accessor to the integer y-axis ticks flag.
Accessor to the legend's corner.
Accessor to the legends' font size of the Drawables inside the Graph.
Accessor to the legend's position of the Drawables inside the Graph.
Accessor to the legends of the Drawables inside the Graph.
Accessor to the indication of axes' scale of the Graph.
getName()Accessor to the object's name.
Accessor to the ticks location flag.
getTitle()Accessor to the title of the Graph.
Accessor to the title of the X axe.
Accessor to the title of the Y axe.
setAutomaticBoundingBox(automaticBoundingBox)Accessor to the indication of automatic bounding box.
setAxes(showAxes)Accessor to the indication of axes' presence on the Graph.
setBoundingBox(boundingBox)Accessor to the bounding box of the whole plot.
setColors(colors)Update the colors of the Drawables inside the Graph.
Assign colors to a default palette to all the drawables of the Graph.
setDrawable(drawable, index)Accessor to a Drawable included in the Graph.
setDrawables(drawableCollection)Accessor to the Drawables included in the Graph.
setGrid(showGrid)Hide or shows grid of the Graph.
setGridColor(color)Accessor to the indication of grid's color on the Graph.
setIntegerXTick(integerXTick)Accessor to the integer x-axis ticks flag.
setIntegerYTick(integerYTick)Accessor to the integer y-axis ticks flag.
setLegendCorner(corner)Accessor to the legend's corner.
setLegendFontSize(legendFontSize)Accessor to the legend's font size of the Drawables inside the Graph.
setLegendPosition(position)Accessor to the legend's position of the Drawables inside the Graph.
setLegends(legends)Accessor to the legends of the Drawables inside the Graph.
setLogScale(logScale)Accessor to the indication of axes' scale of the Graph.
setName(name)Accessor to the object's name.
setTickLocation(tickLocation)Accessor to the ticks location flag.
setTitle(title)Accessor to the title of the Graph.
setXMargin(xMargin)Accessor to the horizontal margin size.
setXTitle(title)Accessor to the title of the X axe.
setYMargin(yMargin)Accessor to the vertical margin size.
setYTitle(title)Accessor to the title of the Y axe.
- __init__(*args)¶
- static GetValidLegendPositions()¶
Accessor to the list of valid legend positions.
- Returns:
- listPositions
Description All the valid legend positions.
- listPositions
Examples
>>> import openturns as ot >>> print(ot.Graph.GetValidLegendPositions()) [,best,upper right,upper left,lower right,lower left,center right,...
- static IsValidLegendPosition(position)¶
Test if the proposed legend position is valid or not.
- Parameters:
- positionstr
Proposed legend position of the Drawables inside the Graph.
- Returns:
- validitybool
True if the proposed legend position is valid, False if it is not.
See also
Examples
>>> import openturns as ot >>> print(ot.Graph.IsValidLegendPosition('lefttop')) False >>> print(ot.Graph.IsValidLegendPosition('upper left')) True
- add(*args)¶
Add drawable instances to the collection of drawables contained in Graph.
- Available usages:
add(drawables)
add(aGraph)
- Parameters:
Notes
It adds the new drawables or graph inside the first one, with their legend. It keeps the graphical context of the first graph. Each drawable keeps its graphical context. Drawables that do not have an explicitly set color will be assigned the default palette color corresponding to their rank in the graph.
Warning
Different drawables might be colored the same…
- erase(i)¶
Erase a drawable instance from the collection of drawables contained in Graph.
- Parameters:
- indexint
Index of the drawable instance to erase from the collection of drawables contained in Graph.
- getAutomaticBoundingBox()¶
Accessor to the indication of automatic bounding box.
- Returns:
- autoBoundingBoxbool
Indicates if the bounding box is automatically created or not. The bounding box of the drawable element is a rectangle determined by its range along X and its range along Y.
- getAxes()¶
Accessor to the indication of axes’ presence on the Graph.
- Returns:
- axesbool
True if the axes are drawn, False if they are hidden.
- getBoundingBox()¶
Accessor to the bounding box of the whole plot.
- Returns:
- boundingBox
Intervalof dimension 2 Bounding box of the drawable element, which is a rectangle determined by its range along X and its range along Y. This methods adds x/y margins according to the margin attributes.
- boundingBox
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getColors()¶
Accessor to the colors of the Drawables included in the Graph.
- Returns:
- listColors
Description List of all the colors used for the Drawables contained inside the graph.
- listColors
- getDrawable(index)¶
Accessor to a Drawable included in the Graph.
- Parameters:
- indexpositive int
Position of the Drawable.
- Returns:
- drawable
Drawable Drawable included in the Graph at the index.
- drawable
- getDrawables()¶
Accessor to the Drawables included in the Graph.
- Returns:
- drawableslist of
Drawable Drawables included in the Graph.
- drawableslist of
- getGrid()¶
Accessor to the indication of grid’s presence on the Graph.
- Returns:
- showGridbool
True to show the grid of the Graph, False to hide it. By default there is a gray grid.
- getGridColor()¶
Accessor to the indication of grid’s color on the Graph.
- Returns:
- gridColorstr
Color of the grid. By default the grid is gray.
- getId()¶
Accessor to the object’s id.
- Returns:
- idint
Internal unique identifier.
- getImplementation()¶
Accessor to the underlying implementation.
- Returns:
- implImplementation
A copy of the underlying implementation object.
- getIntegerXTick()¶
Accessor to the integer x-axis ticks flag.
- Returns:
- integerXTickbool
Whether to draw only integer ticks on the x-axis.
- getIntegerYTick()¶
Accessor to the integer y-axis ticks flag.
- Returns:
- integerYTickbool
Whether to draw only integer ticks on the y-axis.
- getLegendCorner()¶
Accessor to the legend’s corner.
- Returns:
- corner
Point Relative coordinates (in [0,1]x[0,1]) of the legend in the graph bounding box. The position of the legend relatively to this point will depend on the orientation given by the
getLegendPosition()value.
- corner
- getLegendFontSize()¶
Accessor to the legends’ font size of the Drawables inside the Graph.
- Returns:
- fontSizefloat
Legends’ font size used for the drawables contained inside the Graph.
See also
- getLegendPosition()¶
Accessor to the legend’s position of the Drawables inside the Graph.
- Returns:
- positionstr
Legend’s position used for the drawables contained inside the Graph.
See also
- getLegends()¶
Accessor to the legends of the Drawables inside the Graph.
- Returns:
- legends
Description Legends used for the drawables contained inside the Graph.
- legends
- getLogScale()¶
Accessor to the indication of axes’ scale of the Graph.
- Returns:
- scaleint
Indicates the type of the axes’s scale:
0: no log scale is used,
1: log scale is used only for horizontal data,
2: log scale is used only for vertical data,
3: log scale is used for both data.
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- getTickLocation()¶
Accessor to the ticks location flag.
- Returns:
- locint
Indicates the ticks location.
- getTitle()¶
Accessor to the title of the Graph.
- Returns:
- titlestr
Title of the Graph.
- getXTitle()¶
Accessor to the title of the X axe.
- Returns:
- Xtitlestr
Title of the X axe.
- getYTitle()¶
Accessor to the title of the Y axe.
- Returns:
- Ytitlestr
Title of the Y axe.
- setAutomaticBoundingBox(automaticBoundingBox)¶
Accessor to the indication of automatic bounding box.
- Parameters:
- autoBoundingBoxbool
Indicates if the bounding box is automatically created or not. The bounding box of the drawable element is a rectangle determined by its range along X and its range along Y.
- setAxes(showAxes)¶
Accessor to the indication of axes’ presence on the Graph.
- Parameters:
- axesbool
True to draw the axes, False to hide the axes.
- setBoundingBox(boundingBox)¶
Accessor to the bounding box of the whole plot.
- Parameters:
- boundingBox
Intervalof dimension 2 Bounding box of the drawable element, which is a rectangle determined by its range along X and its range along Y.
- boundingBox
- setColors(colors)¶
Update the colors of the Drawables inside the Graph.
- Parameters:
- listColorssequence of str
List of the colors used for each Drawable of the Graph. If the listColors’s size is lower than the number of Drawables, the first colors of listColors are re-used. If it is greated than the number of Drawables, the last colors of the list are ignored.
The listColors argument can be the result of the static method
BuildDefaultPalette()orBuildTableauPalette()of the Drawable object.
- setDefaultColors()¶
Assign colors to a default palette to all the drawables of the Graph.
Notes
This method ensures that drawables of the Graph have different colors.
- setDrawable(drawable, index)¶
Accessor to a Drawable included in the Graph.
- Parameters:
- drawable
Drawable Drawable included in the Graph.
- indexint
Position of the Drawable.
- drawable
Notes
If the drawable does not have an explicitly set color, it will be assigned the default palette color corresponding to its rank in the graph.
- setDrawables(drawableCollection)¶
Accessor to the Drawables included in the Graph.
- Parameters:
- drawableslist of
Drawable Drawables included in the Graph.
- drawableslist of
Notes
Drawables that do not have an explicitly set color will be assigned the default palette color corresponding to their rank in the graph.
- setGrid(showGrid)¶
Hide or shows grid of the Graph.
- Parameters:
- showGridbool
True to show the grid of the Graph, False to hide it.
- setGridColor(color)¶
Accessor to the indication of grid’s color on the Graph.
- Parameters:
- gridColorstr
Color of the grid. By default the grid is gray.
- setIntegerXTick(integerXTick)¶
Accessor to the integer x-axis ticks flag.
- Parameters:
- integerXTickbool
Whether to draw only integer ticks on the x-axis.
- setIntegerYTick(integerYTick)¶
Accessor to the integer y-axis ticks flag.
- Parameters:
- integerYTickbool
Whether to draw only integer ticks on the y-axis.
- setLegendCorner(corner)¶
Accessor to the legend’s corner.
- Parameters:
- cornersequence of float
Relative coordinates (in [0,1]x[0,1]) of the legend in the graph bounding box. The position of the legend relatively to this point will depend on the orientation given by the
getLegendPosition()value.
Notes
This enables the legend to be located outside the graph.
Examples
>>> import openturns as ot >>> position = 'upper left' # the legend's upper left corner with be set below >>> graph = ot.Graph('Some curves', 'x1', 'x2', True, position, 1.0, 0) >>> graph.setLegendCorner([1.0, 1.0]) # legend will begin in top right corner
- setLegendFontSize(legendFontSize)¶
Accessor to the legend’s font size of the Drawables inside the Graph.
- Parameters:
- fontSizefloat
Legend’s font size used for the drawables contained inside the Graph.
Examples
>>> import openturns as ot >>> fontSize = 1.0 >>> # Create an empty graph >>> myGraph = ot.Graph('Some curves', 'x1', 'x2', True, 'upper right', fontSize, 0) >>> myGraph.setLegendFontSize(1.5) >>> print(myGraph.getLegendFontSize()) 1.5
- setLegendPosition(position)¶
Accessor to the legend’s position of the Drawables inside the Graph.
- Parameters:
- positionstr
Legend’s position used for the drawables contained inside the Graph. The valid positions are given by the method
GetValidLegendPositions().
Examples
>>> import openturns as ot >>> position = 'upper right' >>> # Create an empty graph >>> myGraph = ot.Graph('Some curves', 'x1', 'x2', True, position, 1.0, 0) >>> myGraph.setLegendPosition('lower left') >>> print(myGraph.getLegendPosition()) lower left
- setLegends(legends)¶
Accessor to the legends of the Drawables inside the Graph.
- Parameters:
- legendssequence of str
Legends used for the drawables contained inside the Graph.
- setLogScale(logScale)¶
Accessor to the indication of axes’ scale of the Graph.
- Parameters:
- scaleint
Indicates the type of the axes’s scale:
ot.GraphImplementation.NONE or 0: no log scale is used,
ot.GraphImplementation.LOGX or 1: log scale is used only for horizontal data,
ot.GraphImplementation.LOGY or 2: log scale is used only for vertical data,
ot.GraphImplementation.LOGXY or 3: log scale is used for both data.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
- setTickLocation(tickLocation)¶
Accessor to the ticks location flag.
- Parameters:
- locint
Indicates the ticks location:
ot.GraphImplementation.TICKNONE: no ticks,
ot.GraphImplementation.TICKX: horizontal ticks,
ot.GraphImplementation.TICKY: vertical ticks,
ot.GraphImplementation.TICKXY: horizontal and vertical ticks.
- setTitle(title)¶
Accessor to the title of the Graph.
- Parameters:
- titlestr
Title of the Graph.
- setXMargin(xMargin)¶
Accessor to the horizontal margin size.
- Parameters:
- xMarginfloat
Horizontal margin ratio, defaults to 5% of the range on each side. In log-scale, it is interpreted as a power of 10; setting a value of 1 means a margin of one decade on each side. Defaults to Graph-DefaultHorizontalMargin map value.
- setXTitle(title)¶
Accessor to the title of the X axe.
- Parameters:
- Xtitlestr
Title of the X axe.
- setYMargin(yMargin)¶
Accessor to the vertical margin size.
- Parameters:
- yMarginfloat
Vertical margin ratio, defaults to 5% of the range on each side. In log-scale, it is interpreted as a power of 10; setting a value of 1 means a margin of one decade on each side. Defaults to Graph-DefaultVerticalMargin map value.
- setYTitle(title)¶
Accessor to the title of the Y axe.
- Parameters:
- Ytitlestr
Title of the Y axe.
Examples using the class¶
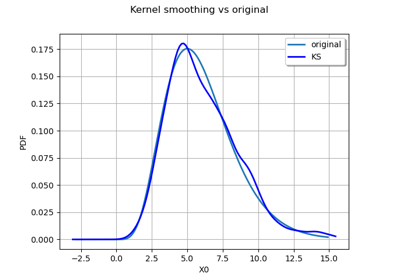
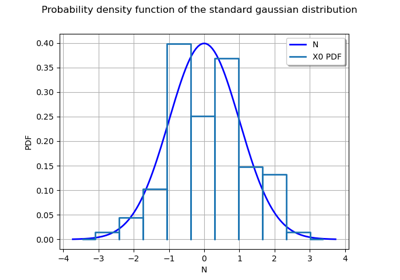
Kolmogorov-Smirnov : get the statistics distribution
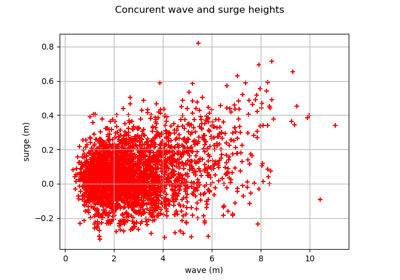
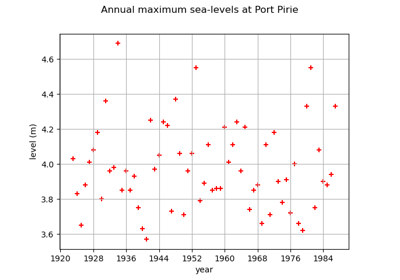
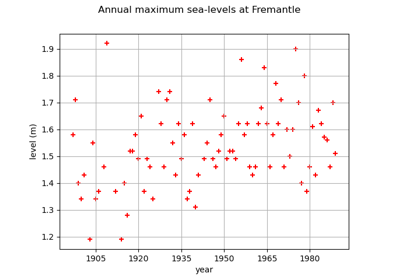
Estimate tail dependence coefficients on the wave-surge data
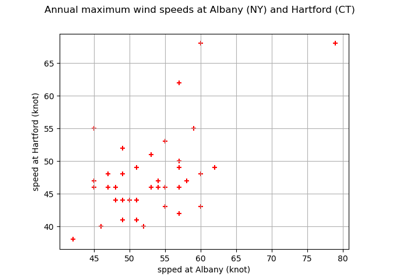
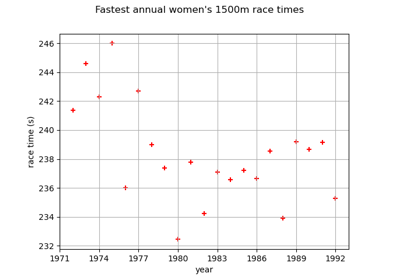
Estimate tail dependence coefficients on the wind data
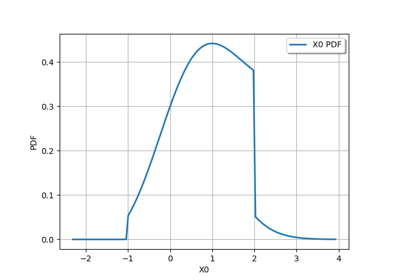
Create the distribution of the maximum of independent distributions
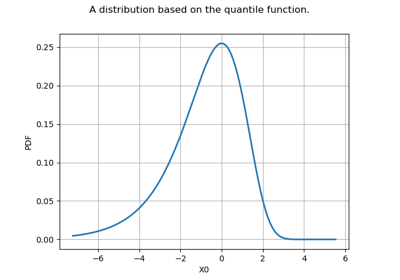
Create your own distribution given its quantile function
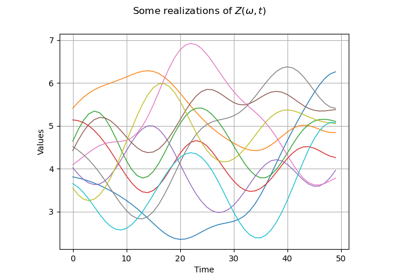
Create a gaussian process from a cov. model using HMatrix
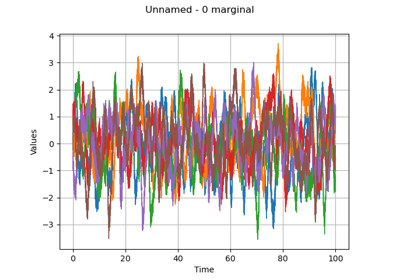
Create a process from random vectors and processes
Sample trajectories from a Gaussian Process with correlated outputs
Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos
Example of multi output Kriging on the fire satellite model
Kriging: choose a polynomial trend on the beam model
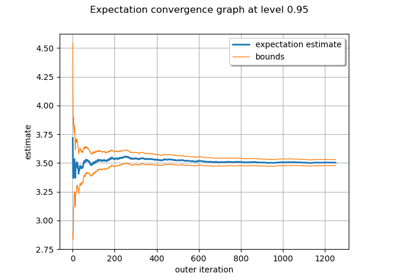
Evaluate the mean of a random vector by simulations
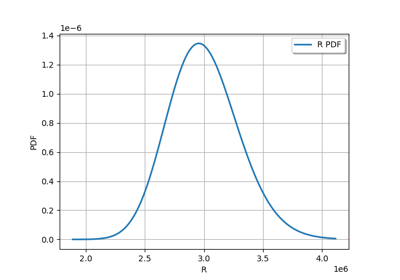
Estimate a probability with Monte-Carlo on axial stressed beam: a quick start guide to reliability
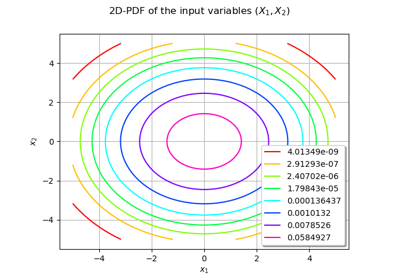
Use the FORM algorithm in case of several design points
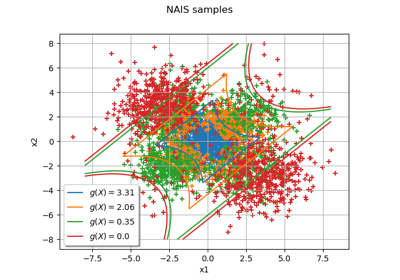
Non parametric Adaptive Importance Sampling (NAIS)
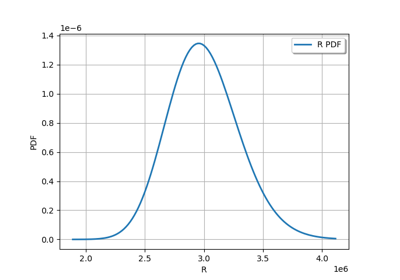
Axial stressed beam : comparing different methods to estimate a probability
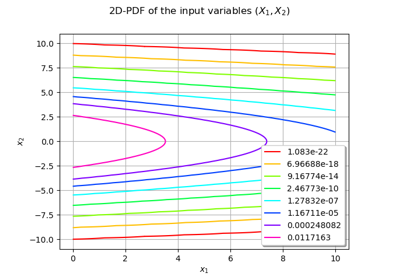
An illustrated example of a FORM probability estimate
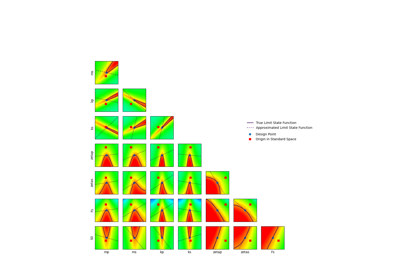
Using the FORM - SORM algorithms on a nonlinear function
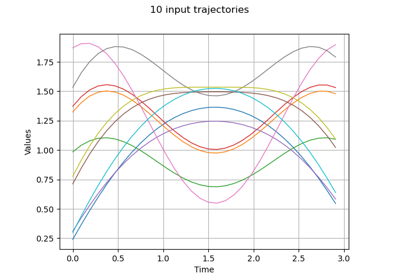
Estimate Sobol indices on a field to point function
Estimate Sobol’ indices for a function with multivariate output
Example of sensitivity analyses on the wing weight model
Create mixed deterministic and probabilistic designs of experiments
Create a design of experiments with discrete and continuous variables
Define a function with a field output: the viscous free fall example
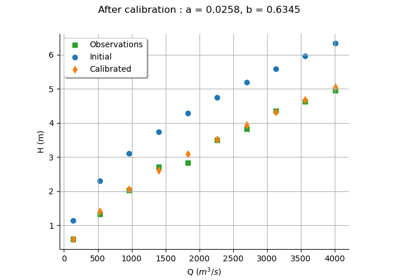
Calibrate a parametric model: a quick-start guide to calibration
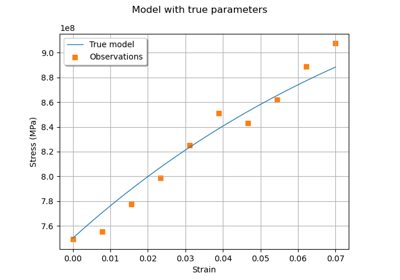
Generate observations of the Chaboche mechanical model
Linear Regression with interval-censored observations
Compute leave-one-out error of a polynomial chaos expansion
Compute confidence intervals of a regression model from data
Compute confidence intervals of a univariate noisy function
Plot the log-likelihood contours of a distribution
 OpenTURNS
OpenTURNS