InterfaceObject¶
- class InterfaceObject(*args, **kwargs)¶
Methods
Accessor to the object's name.
getId()Accessor to the object's id.
getName()Accessor to the object's name.
setName(name)Accessor to the object's name.
- __init__(*args, **kwargs)¶
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getId()¶
Accessor to the object’s id.
- Returns:
- idint
Internal unique identifier.
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
Examples using the class¶

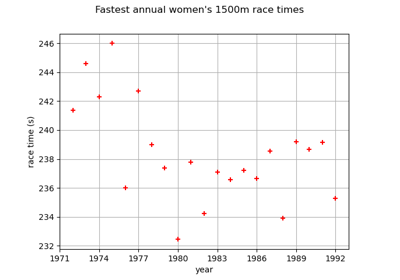
A quick start guide to the Point and Sample classes
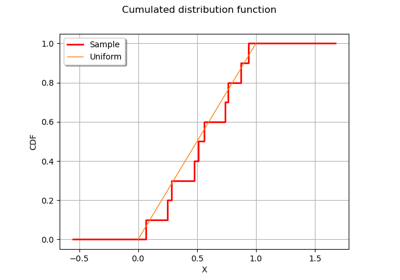
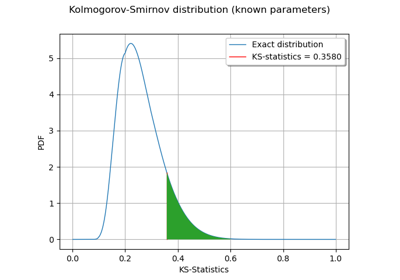
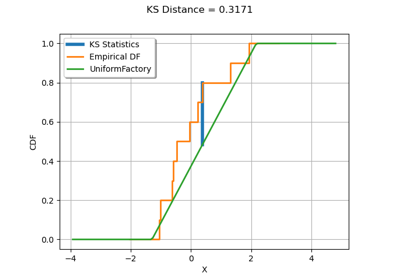
Kolmogorov-Smirnov : get the statistics distribution
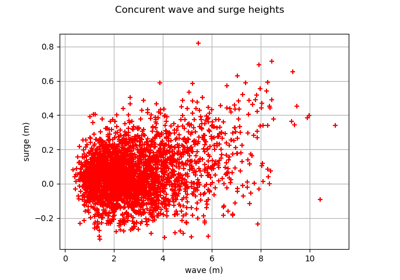
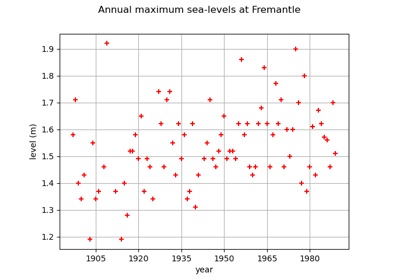
Estimate tail dependence coefficients on the wave-surge data
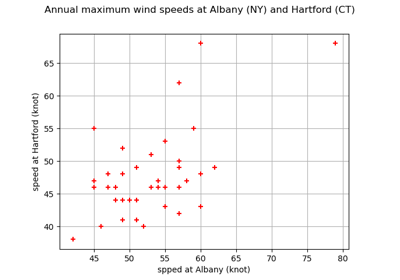
Estimate tail dependence coefficients on the wind data
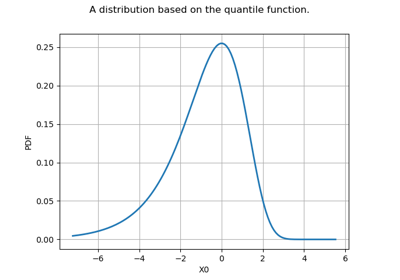
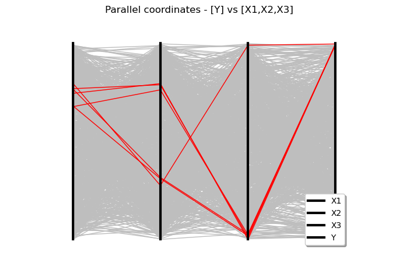
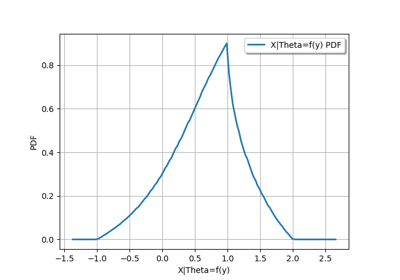
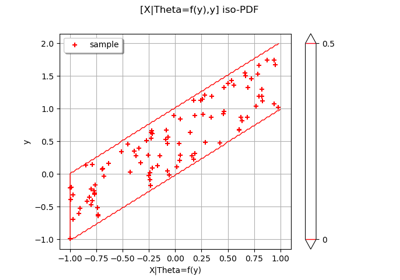
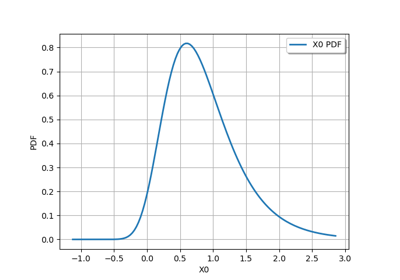
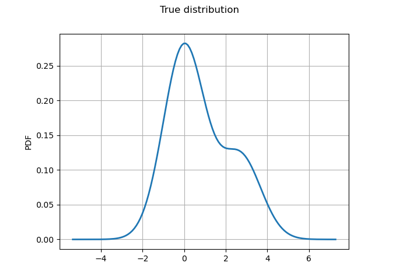
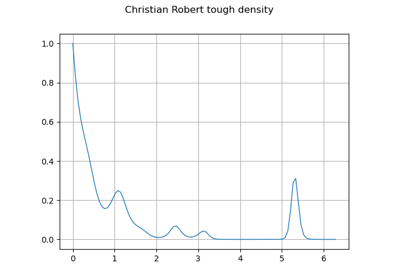
Create your own distribution given its quantile function
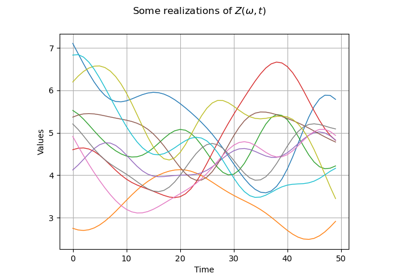
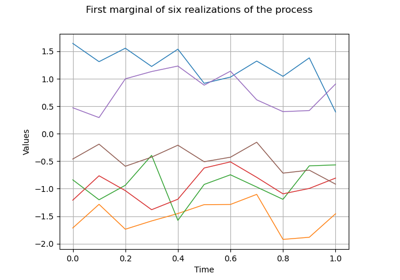
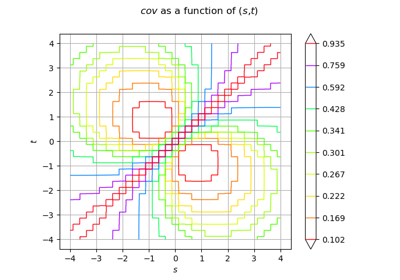
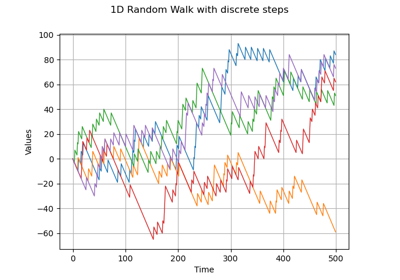
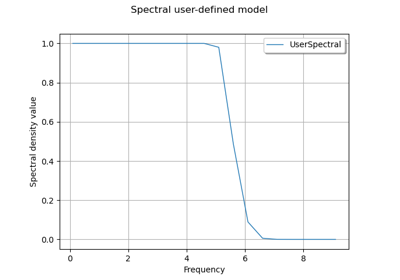
Create a process from random vectors and processes
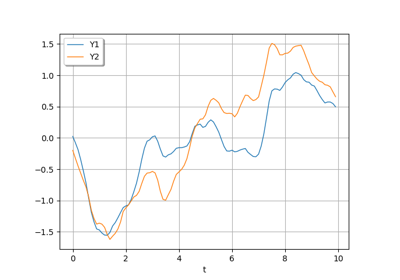
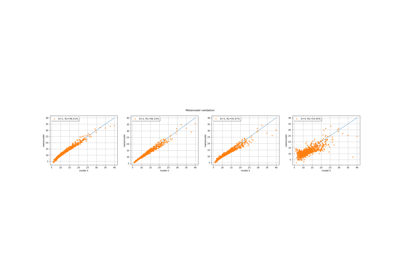
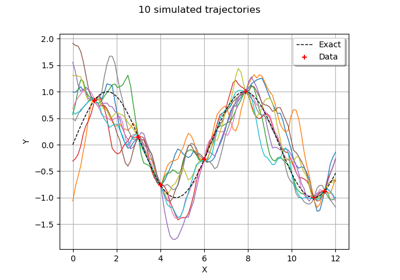
Sample trajectories from a Gaussian Process with correlated outputs

Apply a transform or inverse transform on your polynomial chaos

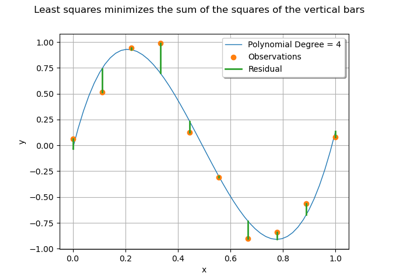
Create a full or sparse polynomial chaos expansion
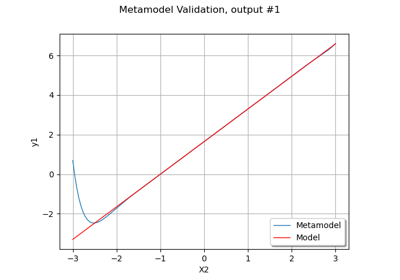
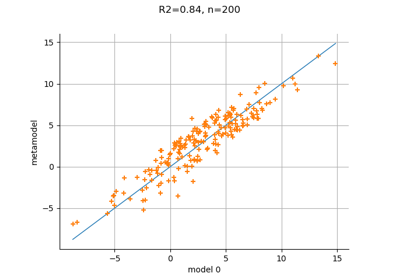
Create a polynomial chaos metamodel from a data set
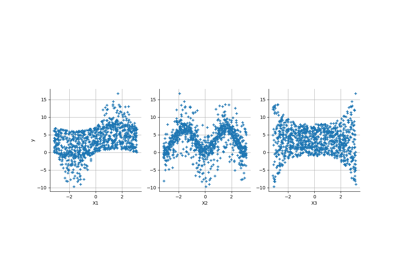
Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos
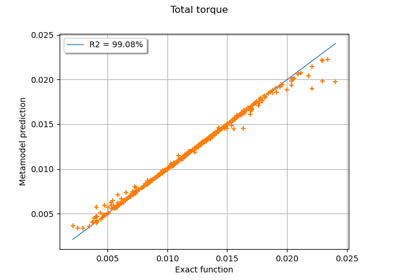
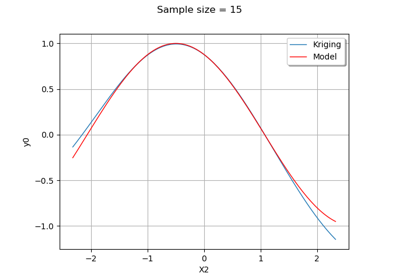
Example of multi output Kriging on the fire satellite model
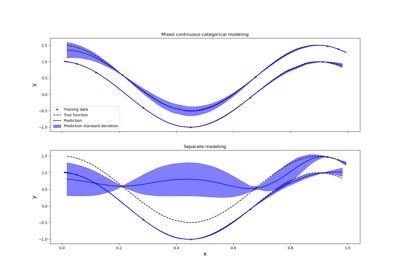
Kriging: metamodel with continuous and categorical variables
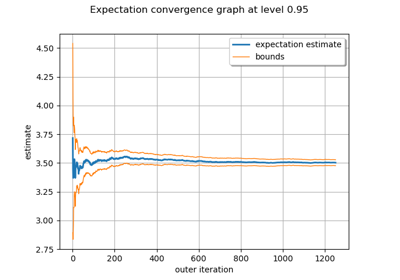
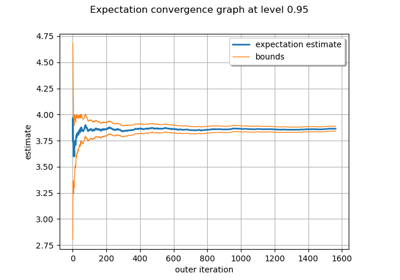
Evaluate the mean of a random vector by simulations

Use the Adaptive Directional Stratification Algorithm

Use the post-analytical importance sampling algorithm
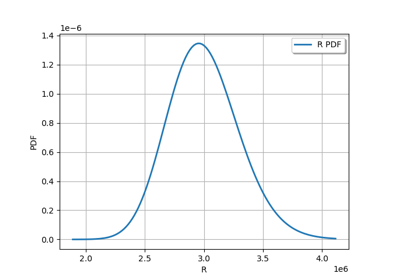
Estimate a probability with Monte-Carlo on axial stressed beam: a quick start guide to reliability
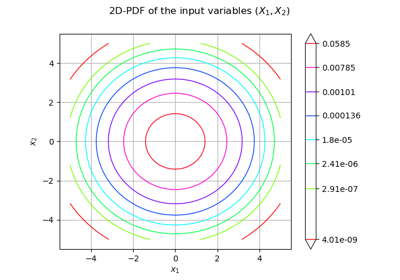
Use the FORM algorithm in case of several design points
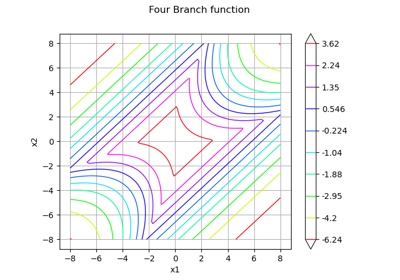
Non parametric Adaptive Importance Sampling (NAIS)

Test the design point with the Strong Maximum Test
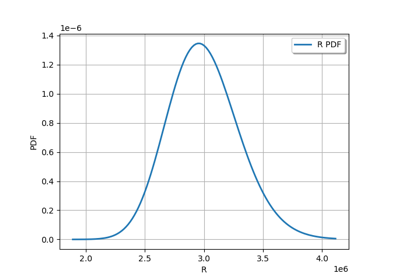
Axial stressed beam : comparing different methods to estimate a probability
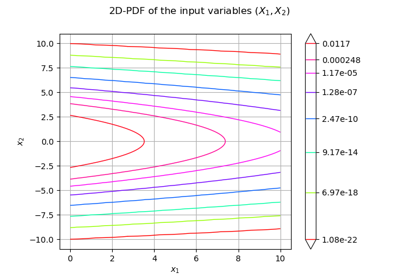
An illustrated example of a FORM probability estimate
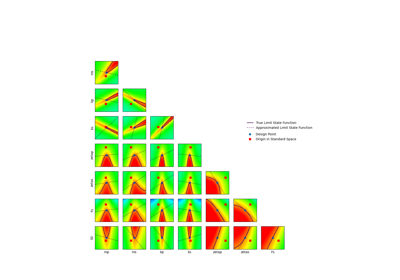
Using the FORM - SORM algorithms on a nonlinear function
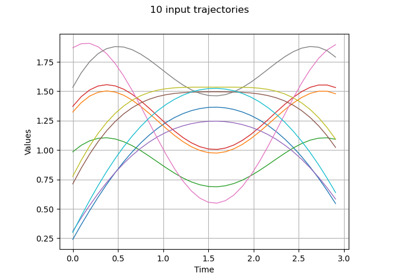
Estimate Sobol indices on a field to point function
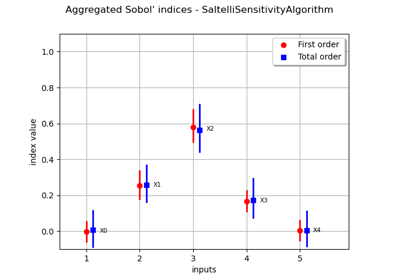
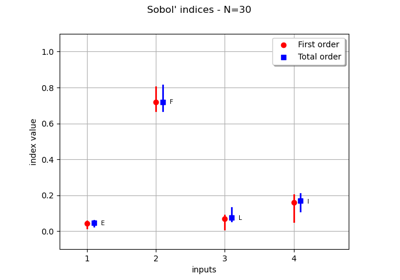
Estimate Sobol’ indices for a function with multivariate output
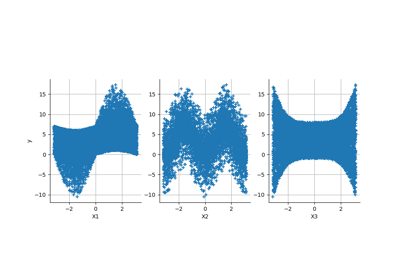
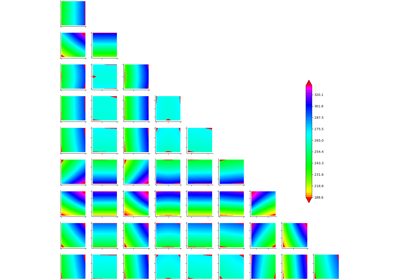
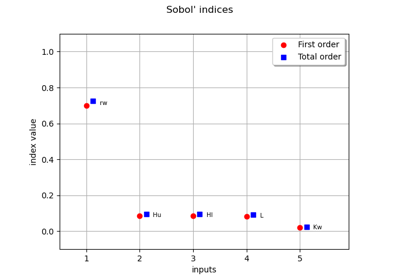
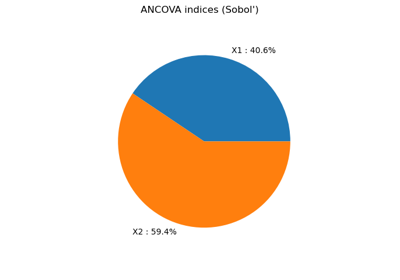
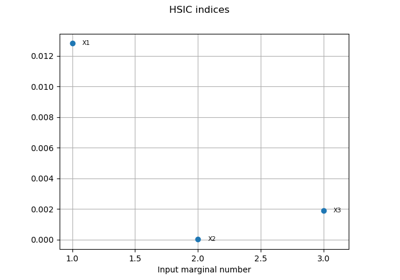
Example of sensitivity analyses on the wing weight model
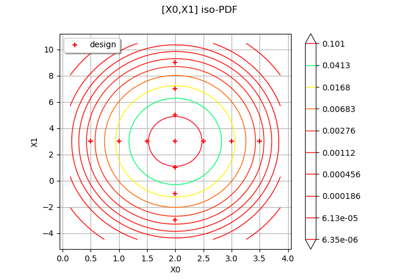
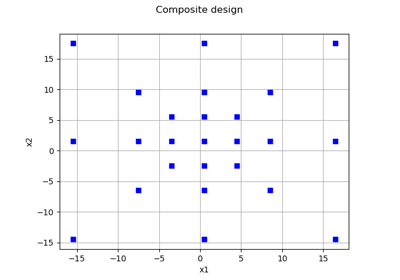
Create mixed deterministic and probabilistic designs of experiments
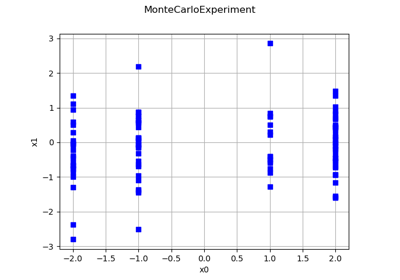
Create a design of experiments with discrete and continuous variables

Defining Python and symbolic functions: a quick start introduction to functions

Create a multivariate basis of functions from scalar multivariable functions
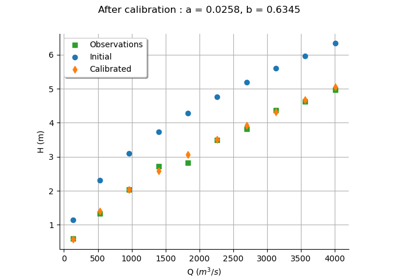
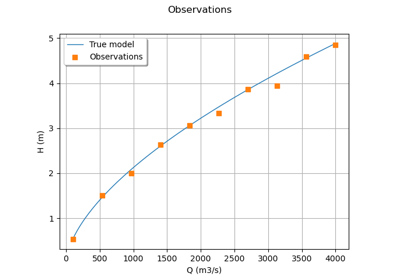
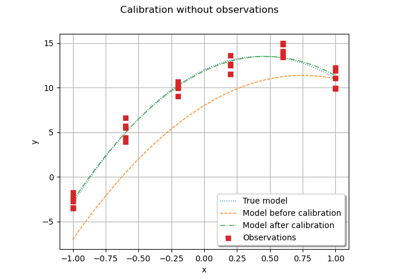
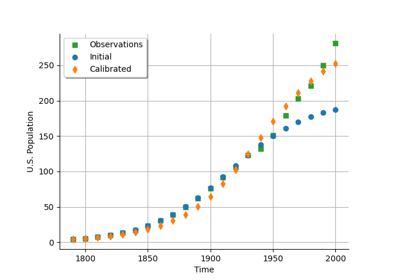
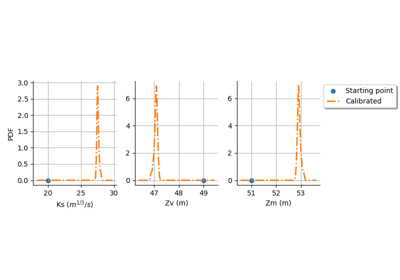
Calibrate a parametric model: a quick-start guide to calibration
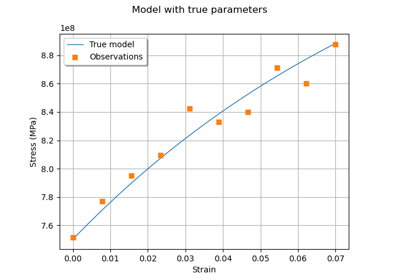
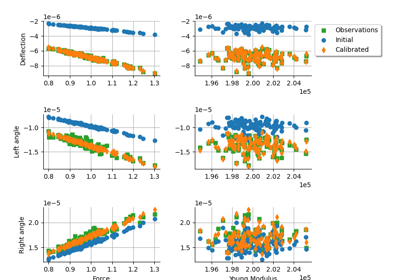
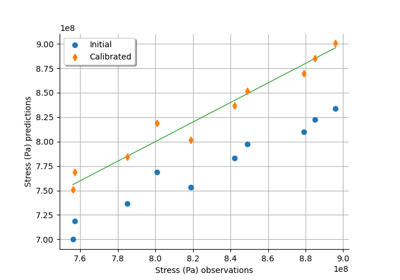
Generate observations of the Chaboche mechanical model
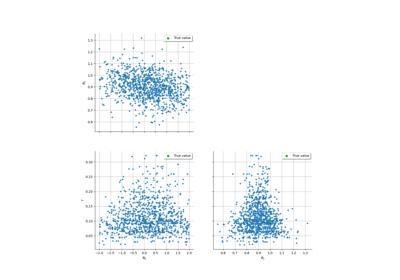
Linear Regression with interval-censored observations
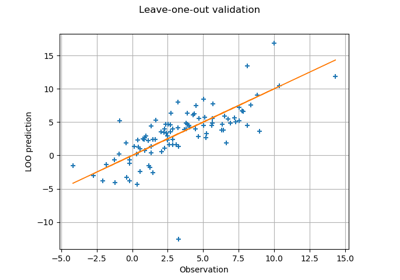
Compute leave-one-out error of a polynomial chaos expansion
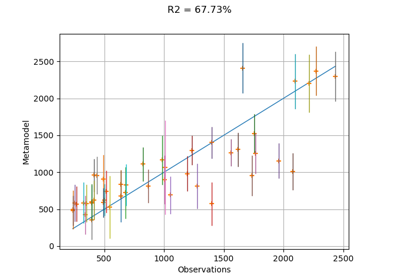
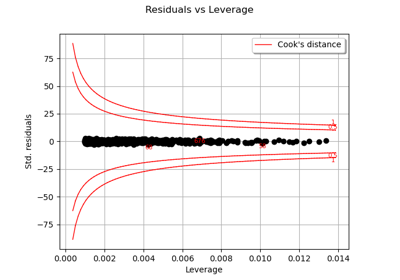
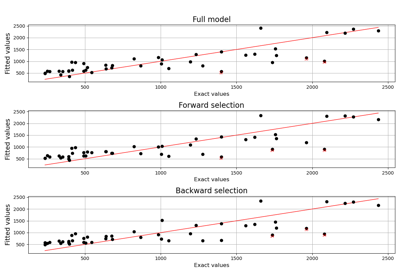
Compute confidence intervals of a regression model from data
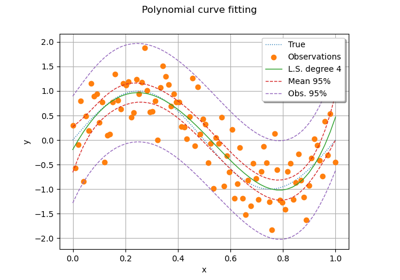
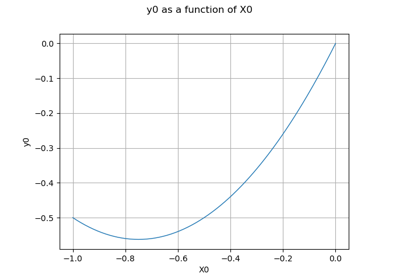
Compute confidence intervals of a univariate noisy function
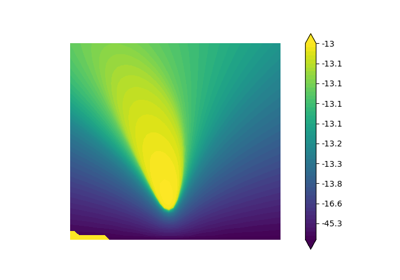
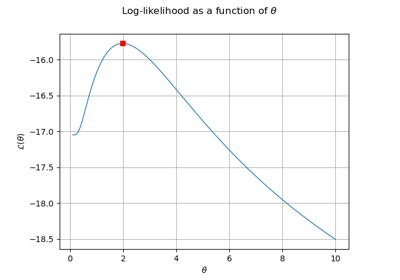
Plot the log-likelihood contours of a distribution
 OpenTURNS
OpenTURNS