PersistentObject¶
- class PersistentObject(*args, **kwargs)¶
PersistentObject saves and reloads the object’s internal state.
Methods
Accessor to the object's name.
getName()Accessor to the object's name.
hasName()Test if the object is named.
setName(name)Accessor to the object's name.
- __init__(*args, **kwargs)¶
- getClassName()¶
Accessor to the object’s name.
- Returns:
- class_namestr
The object class name (object.__class__.__name__).
- getName()¶
Accessor to the object’s name.
- Returns:
- namestr
The name of the object.
- hasName()¶
Test if the object is named.
- Returns:
- hasNamebool
True if the name is not empty.
- setName(name)¶
Accessor to the object’s name.
- Parameters:
- namestr
The name of the object.
Examples using the class¶

A quick start guide to the Point and Sample classes

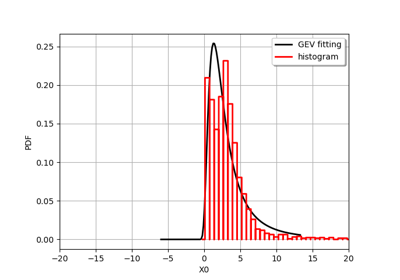
Fitting a distribution with customized maximum likelihood
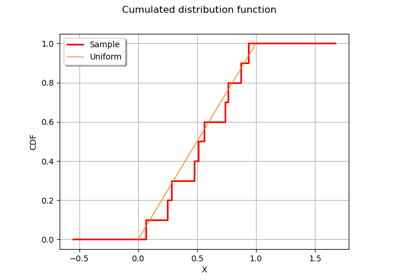
Kolmogorov-Smirnov : get the statistics distribution
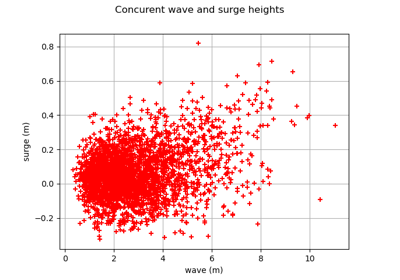
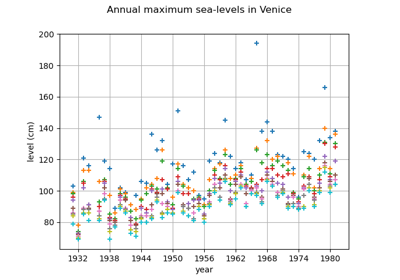
Estimate tail dependence coefficients on the wave-surge data
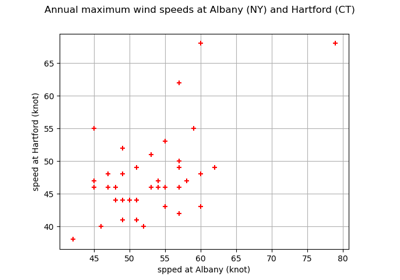
Estimate tail dependence coefficients on the wind data
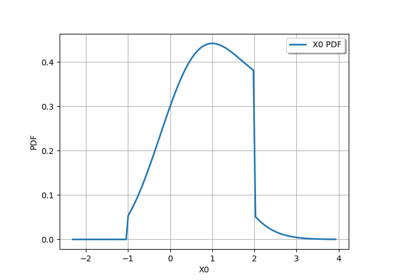
Create the distribution of the maximum of independent distributions
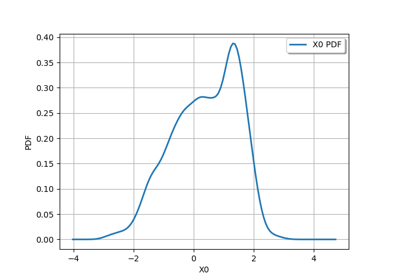
Create your own distribution given its quantile function
Create a gaussian process from a cov. model using HMatrix
Create a process from random vectors and processes
Sample trajectories from a Gaussian Process with correlated outputs

Apply a transform or inverse transform on your polynomial chaos

Create a full or sparse polynomial chaos expansion
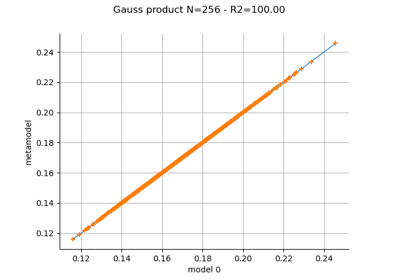
Create a polynomial chaos metamodel by integration on the cantilever beam
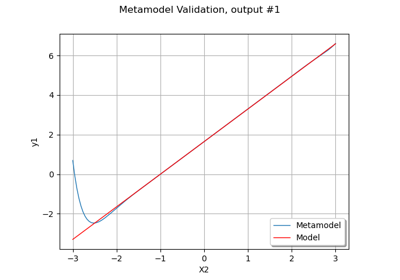
Create a polynomial chaos metamodel from a data set
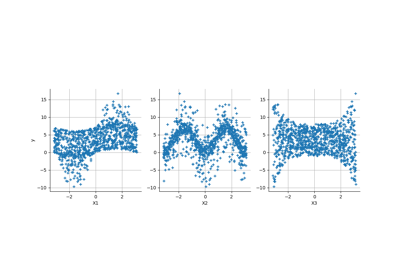
Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos
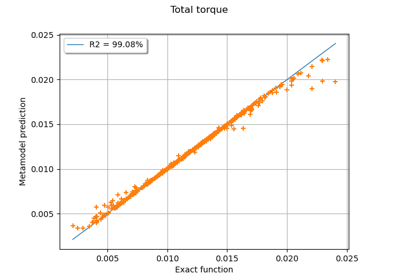
Example of multi output Kriging on the fire satellite model
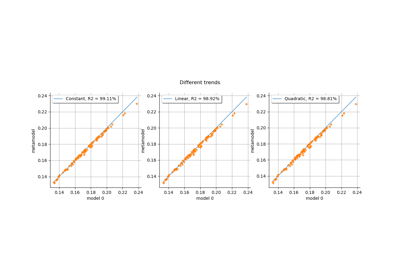
Kriging: choose a polynomial trend on the beam model
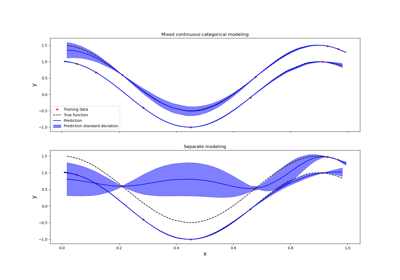
Kriging: metamodel with continuous and categorical variables
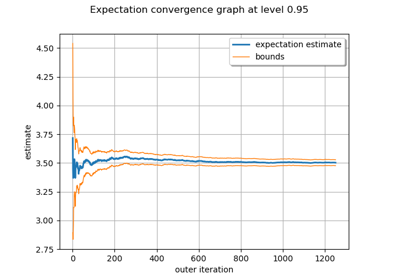
Evaluate the mean of a random vector by simulations

Use the Adaptive Directional Stratification Algorithm

Use the post-analytical importance sampling algorithm
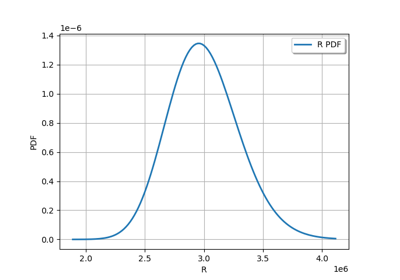
Estimate a probability with Monte-Carlo on axial stressed beam: a quick start guide to reliability
Use the FORM algorithm in case of several design points
Non parametric Adaptive Importance Sampling (NAIS)

Test the design point with the Strong Maximum Test
Axial stressed beam : comparing different methods to estimate a probability
An illustrated example of a FORM probability estimate
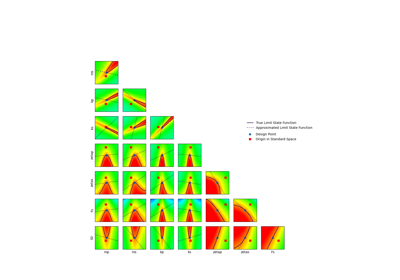
Using the FORM - SORM algorithms on a nonlinear function
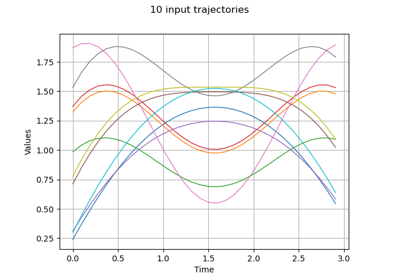
Estimate Sobol indices on a field to point function
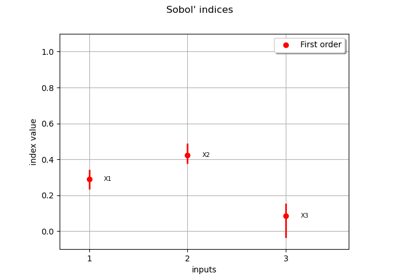
Sobol’ sensitivity indices using rank-based algorithm
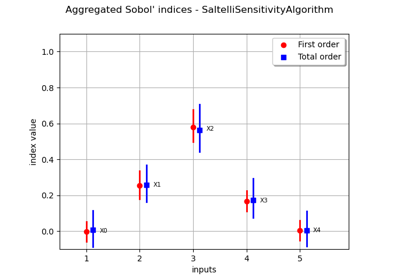
Estimate Sobol’ indices for a function with multivariate output
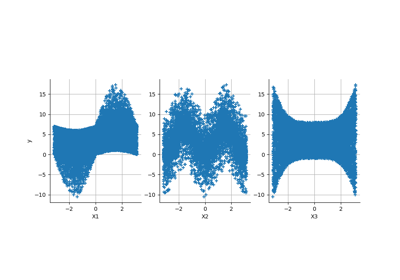
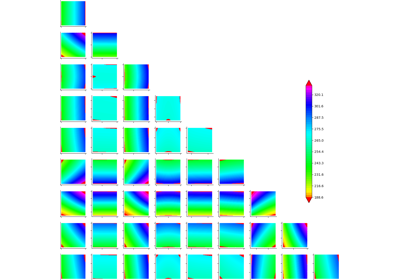
Example of sensitivity analyses on the wing weight model
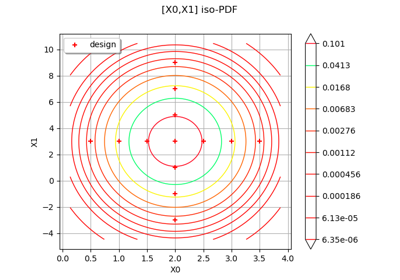
Create mixed deterministic and probabilistic designs of experiments
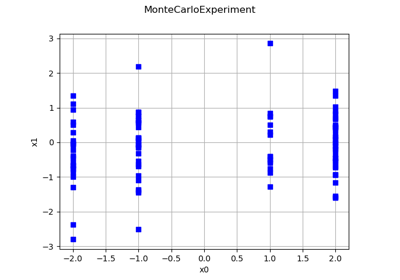
Create a design of experiments with discrete and continuous variables

Defining Python and symbolic functions: a quick start introduction to functions

Create a multivariate basis of functions from scalar multivariable functions
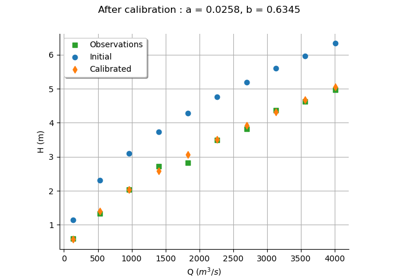
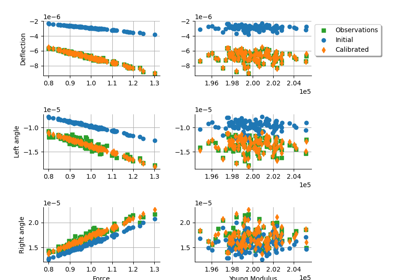
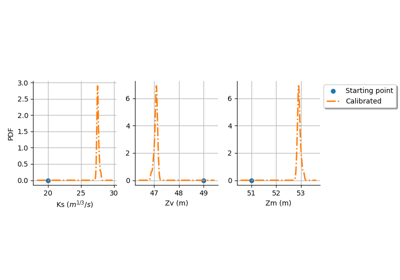
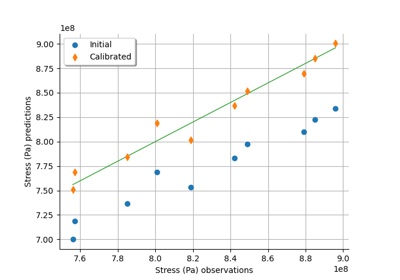
Calibrate a parametric model: a quick-start guide to calibration
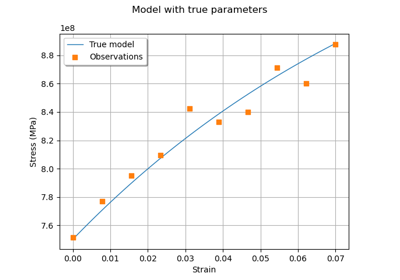
Generate observations of the Chaboche mechanical model
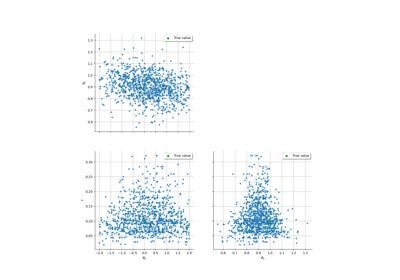
Linear Regression with interval-censored observations
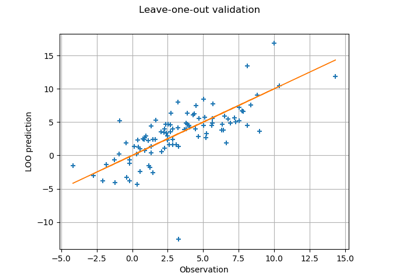
Compute leave-one-out error of a polynomial chaos expansion
Compute confidence intervals of a regression model from data
Compute confidence intervals of a univariate noisy function
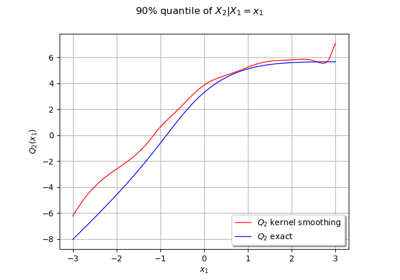
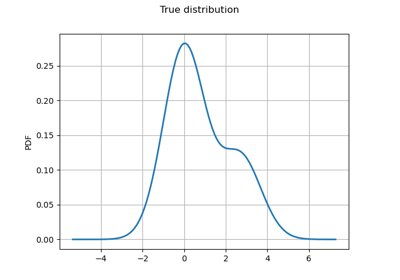
Plot the log-likelihood contours of a distribution
 OpenTURNS
OpenTURNS