View

(Source code, png, hires.png, pdf)

class View(graph, pixelsize=None, figure=None, figure_kw=None, axes=[], plot_kw=None, axes_kw=None, bar_kw=None, pie_kw=None, polygon_kw=None, polygoncollection_kw=None, contour_kw=None, step_kw=None, clabel_kw=None, text_kw=None, legend_kw=None, add_legend=True, square_axes=False, **kwargs)

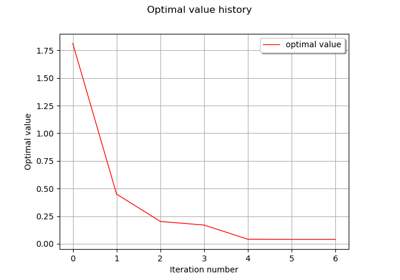
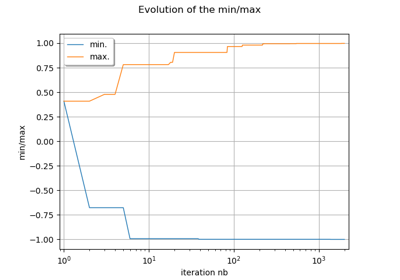
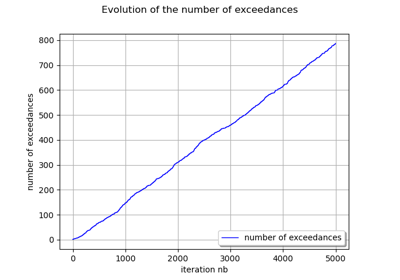
Create the figure.

Parameters:

graphGraph, Drawable or GridLayout

An object to draw.

pixelsize2-tuple of int

The requested size in pixels (width, height).

figurematplotlib.figure.Figure

The figure to draw on.

figure_kwdict, optional

Passed on to matplotlib.pyplot.figure kwargs

axesmatplotlib.axes.Axes

The axes to draw on.

plot_kwdict, optional

Used when drawing Cloud, Curve drawables Passed on as matplotlib.axes.Axes.plot kwargs

axes_kwdict, optional

Passed on to matplotlib.figure.Figure.add_subplot kwargs

bar_kwdict, optional

Used when drawing BarPlot drawables Passed on to matplotlib.pyplot.bar kwargs

pie_kwdict, optional

Used when drawing Pie drawables Passed on to matplotlib.pyplot.pie kwargs

polygon_kwdict, optional

Used when drawing Polygon drawables Passed on to matplotlib.patches.Polygon kwargs

polygoncollection_kwdict, optional

Used when drawing PolygonArray drawables Passed on to matplotlib.collection.PolygonCollection kwargs

contour_kwdict, optional

Used when drawing Contour drawables Passed on to matplotlib.pyplot.contour kwargs

clabel_kwdict, optional

Used when drawing Contour drawables Passed on to matplotlib.pyplot.clabel kwargs

step_kwdict, optional

Used when drawing Staircase drawables Passed on to matplotlib.pyplot.step kwargs

text_kwdict, optional

Used when drawing Pairs, Text drawables Passed on to matplotlib.axes.Axes.text kwargs

legend_kwdict, optional

Passed on to matplotlib.axes.Axes.legend kwargs

add_legendbool, optional

Adds a legend if True. Default is True.

square_axesbool, optional

Forces the axes to share the same scale if True. Default is False.

Examples

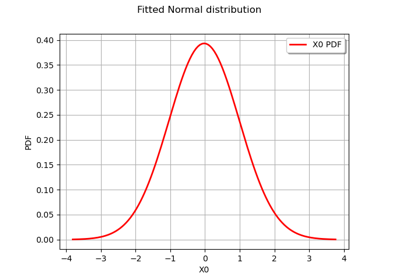
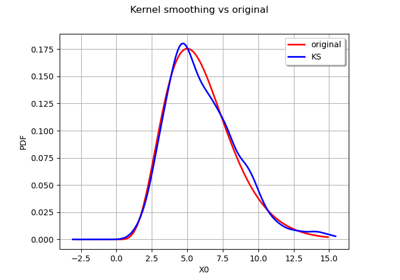
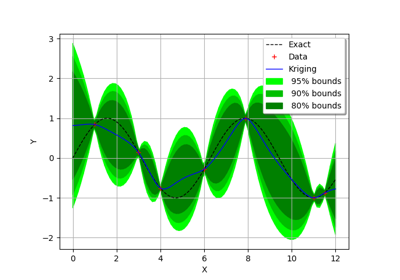
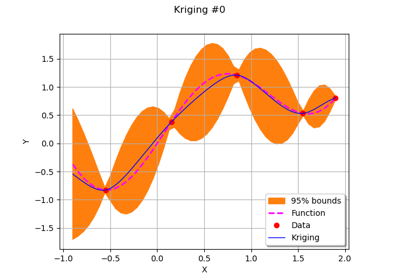
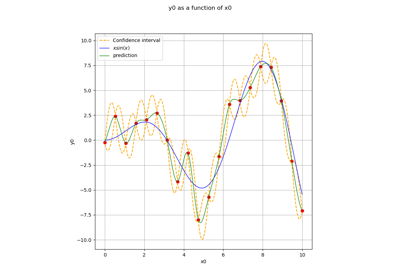
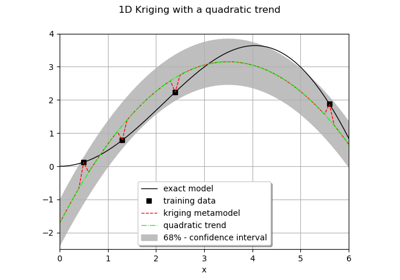
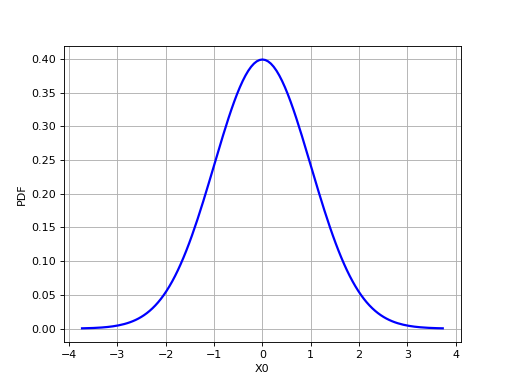
>>> import openturns as ot
>>> from openturns.viewer import View
>>> graph = ot.Normal().drawPDF()
>>> view = View(graph, plot_kw={'color':'blue'})
>>> view.save('graph.png', dpi=100)
>>> view.show()

Methods

ShowAll(**kwargs)	Display all graphs.
close()	Close the figure.
getAxes()	Get the list of Axes objects.
getFigure()	Accessor to the underlying figure object.
save(fname, **kwargs)	Save the graph as file.
show(**kwargs)	Display the graph.

__init__(graph, pixelsize=None, figure=None, figure_kw=None, axes=[], plot_kw=None, axes_kw=None, bar_kw=None, pie_kw=None, polygon_kw=None, polygoncollection_kw=None, contour_kw=None, step_kw=None, clabel_kw=None, text_kw=None, legend_kw=None, add_legend=True, square_axes=False, **kwargs)

static ShowAll(**kwargs)

Display all graphs.

Examples

>>> import openturns as ot
>>> import openturns.viewer as otv
>>> n = ot.Normal()
>>> graph = n.drawPDF()
>>> view = otv.View(graph)
>>> u = ot.Uniform()
>>> graph = u.drawPDF()
>>> view = otv.View(graph)
>>> otv.View.ShowAll()

close()

Close the figure.

Examples

>>> import openturns as ot
>>> import openturns.viewer as otv
>>> n = ot.Normal()
>>> graph = n.drawPDF()
>>> view = otv.View(graph)
>>> view.close()

getAxes()

Get the list of Axes objects.

See matplotlib.axes.Axes for further information.

Examples

>>> import openturns as ot
>>> import openturns.viewer as otv
>>> n = ot.Normal()
>>> graph = n.drawPDF()
>>> view = otv.View(graph)
>>> axes = view.getAxes()
>>> _ = axes[0].set_ylim(-0.1, 1.0);

getFigure()

Accessor to the underlying figure object.

See matplotlib.figure.Figure for further information.

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> graph = ot.Normal().drawPDF()
>>> view = View(graph)
>>> fig = view.getFigure()
>>> _ = fig.suptitle("The suptitle");

save(fname, **kwargs)

Save the graph as file.

Parameters:

fname: bool, optional

A string containing a path to a filename from which file format is deduced.

kwargs:

See matplotlib.figure.Figure.savefig documentation for valid keyword arguments.

Examples

>>> import openturns as ot
>>> from openturns.viewer import View
>>> graph = ot.Normal().drawPDF()
>>> view = View(graph)
>>> view.save('graph.png', dpi=100)

show(**kwargs)

Display the graph.

See matplotlib.figure.Figure.show

Examples

>>> import openturns as ot
>>> import openturns.viewer as otv
>>> n = ot.Normal()
>>> graph = n.drawPDF()
>>> view = otv.View(graph)
>>> view.show()

Examples using the class

Estimate Wilks and empirical quantile

Estimate Wilks and empirical quantile

Build and validate a linear model

Build and validate a linear model

Estimate correlation coefficients

Estimate correlation coefficients

Draw an histogram

Draw an histogram

Draw the empirical CDF

Draw the empirical CDF

Compare unconditional and conditional histograms

Compare unconditional and conditional histograms

Compute SRC indices confidence intervals

Compute SRC indices confidence intervals

Draw a survival function

Draw a survival function

Fit a parametric distribution

Fit a parametric distribution

Model a singular multivariate distribution

Model a singular multivariate distribution

Define a distribution from quantiles

Define a distribution from quantiles

Get the asymptotic distribution of the estimators

Get the asymptotic distribution of the estimators

Bandwidth sensitivity in kernel smoothing

Bandwidth sensitivity in kernel smoothing

Fit an extreme value distribution

Fit an extreme value distribution

Estimate a conditional quantile

Estimate a conditional quantile

Fit a non parametric distribution

Fit a non parametric distribution

Draw the QQ-Plot

Draw the QQ-Plot

Test identical distributions

Test identical distributions

Select fitted distributions

Select fitted distributions

Test Normality

Test Normality

Test the copula

Test the copula

Kolmogorov-Smirnov : understand the statistics

Kolmogorov-Smirnov : understand the statistics

Kolmogorov-Smirnov : understand the p-value

Kolmogorov-Smirnov : understand the p-value

Kolmogorov-Smirnov : get the statistics distribution

Kolmogorov-Smirnov : get the statistics distribution

Fit a parametric copula

Fit a parametric copula

Fit a non parametric copula

Fit a non parametric copula

Estimate a non stationary covariance function

Estimate a non stationary covariance function

Estimate a spectral density function

Estimate a spectral density function

Estimate a stationary covariance function

Estimate a stationary covariance function

Visualize pairs

Visualize pairs

Visualize clouds

Visualize clouds

Visualize sensitivity

Visualize sensitivity

Create the distribution of the maximum of independent distributions

Create the distribution of the maximum of independent distributions

Create a maximum entropy statistics distribution

Create a maximum entropy statistics distribution

Create a conditional distribution

Create a conditional distribution

Create your own distribution given its quantile function

Create your own distribution given its quantile function

Create a Bayes distribution

Create a Bayes distribution

Create a mixture of PDFs

Create a mixture of PDFs

Create an extreme value distribution

Create an extreme value distribution

Create and draw scalar distributions

Create and draw scalar distributions

Truncate a distribution

Truncate a distribution

Create a random mixture

Create a random mixture

Create and draw multivariate distributions

Create and draw multivariate distributions

Generate random variates by inverting the CDF

Generate random variates by inverting the CDF

Transform a distribution

Transform a distribution

Overview of univariate distribution management

Overview of univariate distribution management

Distribution manipulation

Distribution manipulation

Quick start guide

Quick start guide

Create a customized distribution or copula

Create a customized distribution or copula

Draw minimum volume level sets

Draw minimum volume level sets

Create the ordinal sum of copulas

Create the ordinal sum of copulas

Create a functional basis process

Create a functional basis process

Add a trend to a process

Add a trend to a process

Export a field to VTK

Export a field to VTK

Create a gaussian process from a cov. model using HMatrix

Create a gaussian process from a cov. model using HMatrix

Aggregate processes

Aggregate processes

Create a white noise process

Create a white noise process

Create a custom covariance model

Create a custom covariance model

Create a discrete Markov chain process

Create a discrete Markov chain process

Manipulate a time series

Manipulate a time series

Use the Box-Cox transformation

Use the Box-Cox transformation

Create a stationary covariance model

Create a stationary covariance model

Create a normal process

Create a normal process

Create a random walk process

Create a random walk process

Create a spectral model

Create a spectral model

Draw a field

Draw a field

Create a process from random vectors and processes

Create a process from random vectors and processes

Sample trajectories from a Gaussian Process with correlated outputs

Sample trajectories from a Gaussian Process with correlated outputs

Draw fields

Draw fields

Create and manipulate an ARMA process

Create and manipulate an ARMA process

Compare covariance models

Compare covariance models

Create a mesh

Create a mesh

Create a linear least squares model

Create a linear least squares model

Create a general linear model metamodel

Create a general linear model metamodel

Taylor approximations

Taylor approximations

Create a linear model

Create a linear model

Mixture of experts

Mixture of experts

Perfom stepwise regression

Perfom stepwise regression

Over-fitting and model selection

Over-fitting and model selection

Validate a polynomial chaos

Validate a polynomial chaos

Polynomial chaos graphs

Polynomial chaos graphs

Create a polynomial chaos metamodel by integration on the cantilever beam

Create a polynomial chaos metamodel by integration on the cantilever beam

Create a polynomial chaos metamodel

Create a polynomial chaos metamodel

Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos

Create a polynomial chaos for the Ishigami function: a quick start guide to polynomial chaos

Plot enumeration rules

Plot enumeration rules

Chaos cross-validation

Chaos cross-validation

Polynomial chaos is sensitive to the degree

Polynomial chaos is sensitive to the degree

Create a sparse chaos by integration

Create a sparse chaos by integration

Compute Sobol’ indices confidence intervals

Compute Sobol' indices confidence intervals

Kriging : propagate uncertainties

Kriging : propagate uncertainties

Kriging : multiple input dimensions

Kriging : multiple input dimensions

Kriging : draw the likelihood

Kriging : draw the likelihood

Kriging : cantilever beam model

Kriging : cantilever beam model

Example of multi output Kriging on the fire satellite model

Example of multi output Kriging on the fire satellite model

Kriging the cantilever beam model using HMAT

Kriging the cantilever beam model using HMAT

Kriging : generate trajectories from a metamodel

Kriging : generate trajectories from a metamodel

Choose the trend basis of a kriging metamodel

Choose the trend basis of a kriging metamodel

Kriging: metamodel of the Branin-Hoo function

Kriging: metamodel of the Branin-Hoo function

Kriging : quick-start

Kriging : quick-start

Sequentially adding new points to a kriging

Sequentially adding new points to a kriging

Advanced kriging

Advanced kriging

Kriging : choose a trend vector space

Kriging : choose a trend vector space

Kriging : draw covariance models

Kriging : draw covariance models

Validation of a Karhunen-Loeve decomposition

Validation of a Karhunen-Loeve decomposition

Viscous free fall: metamodel of a field function

Viscous free fall: metamodel of a field function

Metamodel of a field function

Metamodel of a field function

Evaluate the mean of a random vector by simulations

Evaluate the mean of a random vector by simulations

Analyse the central tendency of a cantilever beam

Analyse the central tendency of a cantilever beam

Estimate moments from Taylor expansions

Estimate moments from Taylor expansions

Use the Directional Sampling Algorithm

Use the Directional Sampling Algorithm

Estimate a flooding probability

Estimate a flooding probability

Use the Importance Sampling algorithm

Use the Importance Sampling algorithm

Create a threshold event

Create a threshold event

Estimate a probability with Monte-Carlo on axial stressed beam: a quick start guide to reliability

Estimate a probability with Monte-Carlo on axial stressed beam: a quick start guide to reliability

Exploitation of simulation algorithm results

Exploitation of simulation algorithm results

Use the FORM algorithm in case of several design points

Use the FORM algorithm in case of several design points

Non parametric Adaptive Importance Sampling (NAIS)

Non parametric Adaptive Importance Sampling (NAIS)

Create a domain event

Create a domain event

Use the FORM - SORM algorithms

Use the FORM - SORM algorithms

Subset Sampling

Subset Sampling

Time variant system reliability problem

Time variant system reliability problem

Axial stressed beam : comparing different methods to estimate a probability

Axial stressed beam : comparing different methods to estimate a probability

Create unions or intersections of events

Create unions or intersections of events

An illustrated example of a FORM probability estimate

An illustrated example of a FORM probability estimate

Estimate a process-based event probability

Estimate a process-based event probability

Estimate Sobol indices on a field to point function

Estimate Sobol indices on a field to point function

FAST sensitivity indices

FAST sensitivity indices

Parallel coordinates graph as sensitivity tool

Parallel coordinates graph as sensitivity tool

Estimate Sobol’ indices for a function with multivariate output

Estimate Sobol' indices for a function with multivariate output

Sobol’ sensitivity indices from chaos

Sobol' sensitivity indices from chaos

Use the ANCOVA indices

Use the ANCOVA indices

Estimate Sobol’ indices for the Ishigami function by a sampling method: a quick start guide to sensitivity analysis

Estimate Sobol' indices for the Ishigami function by a sampling method: a quick start guide to sensitivity analysis

The HSIC sensitivity indices: the Ishigami model

The HSIC sensitivity indices: the Ishigami model

Example of sensitivity analyses on the wing weight model

Example of sensitivity analyses on the wing weight model

Create a composite design of experiments

Create a composite design of experiments

Create a Monte Carlo design of experiments

Create a Monte Carlo design of experiments

Probabilistic design of experiments

Probabilistic design of experiments

Create a Gauss product design

Create a Gauss product design

Create a random design of experiments

Create a random design of experiments

Create mixed deterministic and probabilistic designs of experiments

Create mixed deterministic and probabilistic designs of experiments

Create a design of experiments with discrete and continuous variables

Create a design of experiments with discrete and continuous variables

Deterministic design of experiments

Deterministic design of experiments

Create a deterministic design of experiments

Create a deterministic design of experiments

Generate low discrepancy sequences

Generate low discrepancy sequences

Optimize an LHS design of experiments

Optimize an LHS design of experiments

Create a symbolic function

Create a symbolic function

Create a quadratic function

Create a quadratic function

Define a function with a field output: the viscous free fall example

Define a function with a field output: the viscous free fall example

Define a connection function with a field output

Define a connection function with a field output

Logistic growth model

Logistic growth model

Function manipulation

Function manipulation

Calibration without observed inputs

Calibration without observed inputs

Calibration of the deflection of a tube

Calibration of the deflection of a tube

Calibration of the logistic model

Calibration of the logistic model

Calibration of the Chaboche mechanical model

Calibration of the Chaboche mechanical model

Calibration of the flooding model

Calibration of the flooding model

Gibbs sampling of the posterior distribution

Gibbs sampling of the posterior distribution

Sampling from an unnormalized probability density

Sampling from an unnormalized probability density

Bayesian calibration of a computer code

Bayesian calibration of a computer code

Bayesian calibration of the flooding model

Bayesian calibration of the flooding model

Posterior sampling using a PythonDistribution

Posterior sampling using a PythonDistribution

Customize your Metropolis-Hastings algorithm

Customize your Metropolis-Hastings algorithm

Linear Regression with interval-censored observations

Linear Regression with interval-censored observations

Estimate an integral

Estimate an integral

Iterated Functions System

Iterated Functions System

Optimization with constraints

Optimization with constraints

Optimization using NLopt

Optimization using NLopt

Quick start guide to optimization

Quick start guide to optimization

Multi-objective optimization using Pagmo

Multi-objective optimization using Pagmo

Optimization of the Rastrigin test function

Optimization of the Rastrigin test function

Optimization using dlib

Optimization using dlib

EfficientGlobalOptimization examples

EfficientGlobalOptimization examples

Estimate moments iteratively

Estimate moments iteratively

Estimate extrema iteratively

Estimate extrema iteratively

Estimate threshold exceedance iteratively

Estimate threshold exceedance iteratively

How to fill an area

How to fill an area

Plot the log-likelihood contours of a distribution

Plot the log-likelihood contours of a distribution

A quick start guide to graphs

A quick start guide to graphs